Lesson 10Bases and Heights of Triangles
Let’s use different base-height pairs to find the area of a triangle.
Learning Targets:
- I can identify corresponding pairs of base and height of any triangle.
- When given information about a base of a triangle, I can identify and draw a corresponding height.
10.1 An Area of 12
Draw one triangle with an area of 12 square units. Try to draw a non-right triangle. Be prepared to explain how you know the area of your triangle is 12 square units.
10.2 Hunting for Heights
-
Here are three copies of the same triangle. The triangle is rotated so that the side chosen as the base is at the bottom and is horizontal. Draw a height that corresponds to each base. Use an index card to help you.
Side as the base:
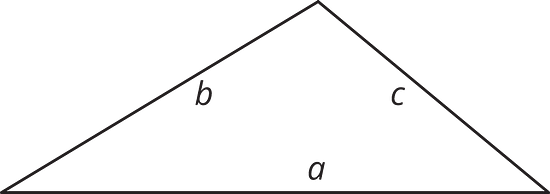
Side as the base:
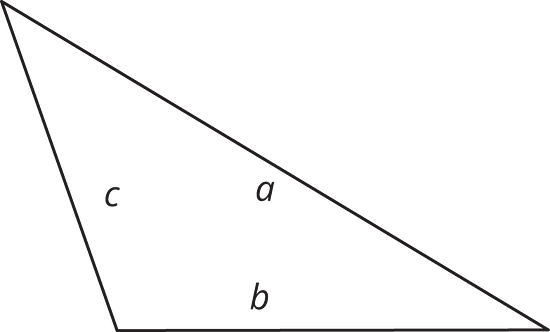
Side as the base:
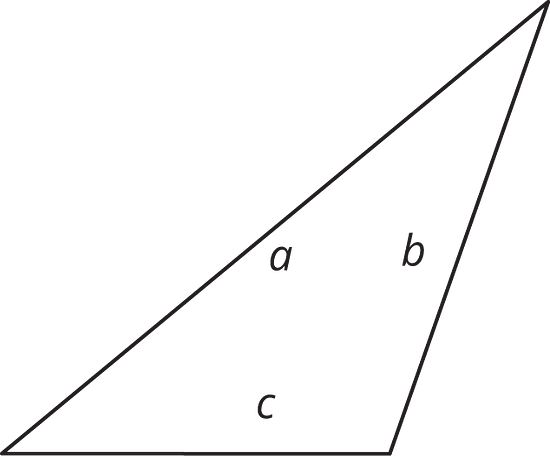
Pause for your teacher’s instructions before moving to the next question.
-
Draw a line segment to show the height for the chosen base in each triangle.
10.3 Some Bases Are Better Than Others
For each triangle, identify and label a base and height. If needed, draw a line segment to show the height.
Then, find the area of the triangle. Show your reasoning. (The side length of each square on the grid is 1 unit.)

Are you ready for more?
Find the area of the triangle below. Show your reasoning.
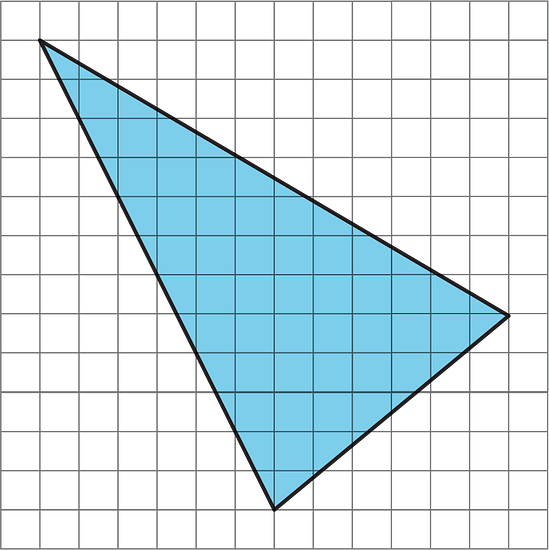
Lesson 10 Summary
A height of a triangle is a perpendicular segment between the side chosen as the base and the opposite vertex. We can use tools with right angles to help us draw height segments.
An index card (or any stiff paper with a right angle) is a handy tool for drawing a line that is perpendicular to another line.
- Choose a side of a triangle as the base. Identify its opposite vertex.
- Line up one edge of the index card with that base.
- Slide the card along the base until a perpendicular edge of the card meets the opposite vertex.
- Use the card edge to draw a line from the vertex to the base. That segment represents the height.
Sometimes we may need to extend the line of the base to identify the height, such as when finding the height of an obtuse triangle, or whenever the opposite vertex is not directly over the base. In these cases, the height segment is typically drawn outside of the triangle.
Even though any side of a triangle can be a base, some base-height pairs can be more easily determined than others, so it helps to choose strategically.
For example, when dealing with a right triangle, it often makes sense to use the two sides that make the right angle as the base and the height because one side is already perpendicular to the other.
If a triangle is on a grid and has a horizontal or a vertical side, you can use that side as a base and use the grid to find the height, as in these examples:
Lesson 10 Practice Problems
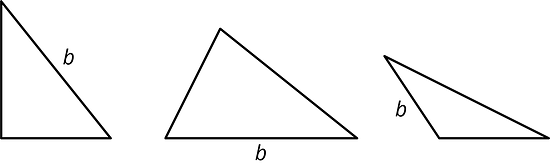
For each triangle, a base is labeled . Draw a line segment that shows its corresponding height. Use an index card to help you draw a straight line.
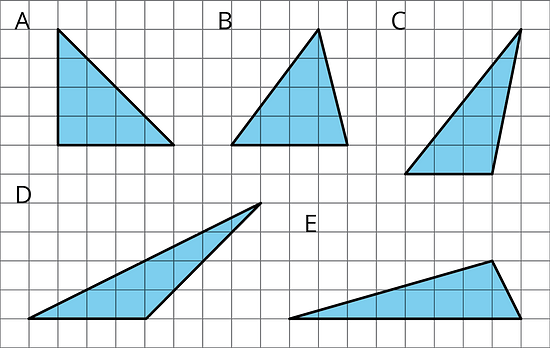
Select all triangles that have an area of 8 square units. Explain how you know.
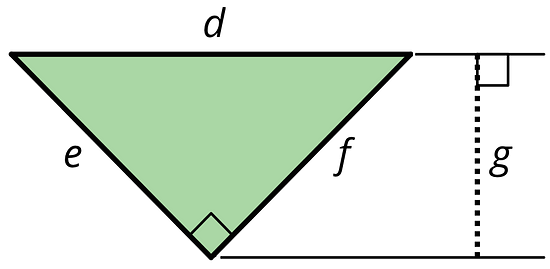
Find the area of the triangle. Show your reasoning.

If you get stuck, carefully consider which side of the triangle to use as the base.
Can side be the base for this triangle? If so, which length would be the corresponding height? If not, explain why not.
Find the area of this shape. Show your reasoning.

On the grid, sketch two different parallelograms that have equal area. Label a base and height of each and explain how you know the areas are the same.
