Lesson 11Polygons
Let’s investigate polygons and their areas.
Learning Targets:
- I can describe the characteristics of a polygon using mathematical vocabulary.
- I can reason about the area of any polygon by decomposing and rearranging it, and by using what I know about rectangles and triangles.
11.1 Which One Doesn’t Belong: Bases and Heights
Which one doesn't belong?
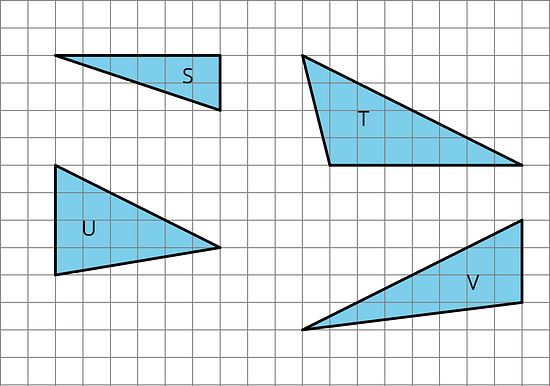
11.2 What Are Polygons?
Here are five polygons:
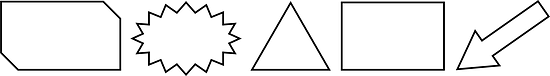
Here are six figures that are not polygons:

-
Circle the figures that are polygons.
-
What do the figures you circled have in common? What characteristics helped you decide whether a figure was a polygon?
11.3 Quadrilateral Strategies
Find the area of two quadrilaterals of your choice. Show your reasoning.
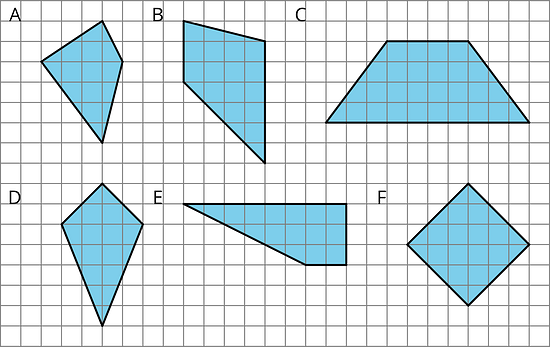
Are you ready for more?
Here is a trapezoid. and represent the lengths of its bottom and top sides. The segment labeled represents its height; it is perpendicular to both the top and bottom sides.
Apply area-reasoning strategies—decomposing, rearranging, duplicating, etc.—on the trapezoid so that you have one or more shapes with areas that you already know how to find.
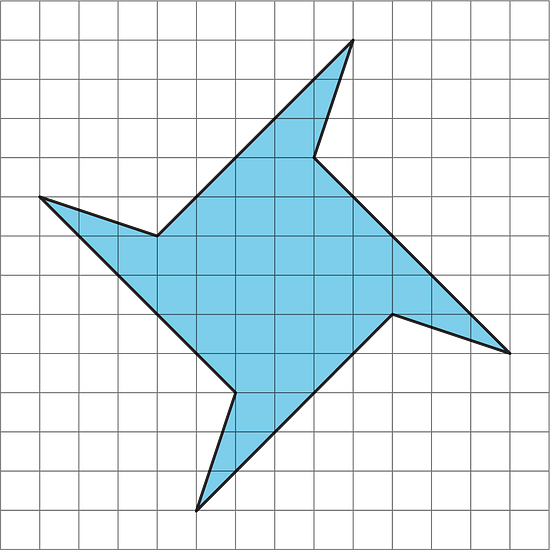
11.4 Pinwheel
Find the area of the shaded region in square units. Show your reasoning.
Lesson 11 Summary
A polygon is a two-dimensional figure composed of straight line segments.
- Each end of a line segment connects to one other line segment. The point where two segments connect is a vertex. The plural of vertex is vertices.
- The segments are called the edges or sides of the polygon. The sides never cross each other. There are always an equal number of vertices and sides.
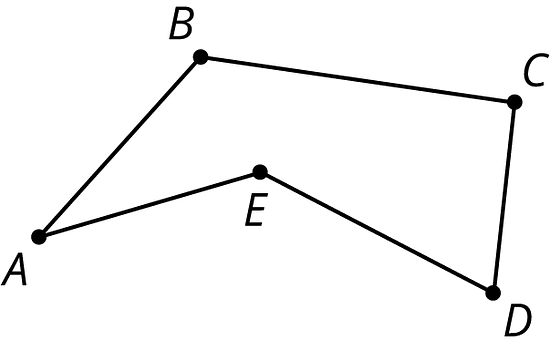
Here is a polygon with 5 sides. The vertices are labeled , and .
A polygon encloses a region. To find the area of a polygon is to find the area of the region inside it.
We can find the area of a polygon by decomposing the region inside it into triangles and rectangles.

The first two diagrams show the polygon decomposed into triangles and rectangles; the sum of their areas is the area of the polygon. The last diagram shows the polygon enclosed in a rectangle; subtracting the areas of the triangles from the area of the rectangle gives us the area of the polygon.
Glossary Terms
Each straight side of a polygon is called an edge.
For example, the edges of this polygon are segments , , , , and .

A polygon is a closed, two-dimensional shape with straight sides that do not cross each other.
Figure is an example of a polygon.

A quadrilateral is a type of polygon that has 4 sides. A rectangle is an example of a quadrilateral. A pentagon is not a quadrilateral, because it has 5 sides.
A vertex is a point where two or more edges meet. When we have more than one vertex, we call them vertices.
The vertices in this polygon are labeled , , , , and .

Lesson 11 Practice Problems
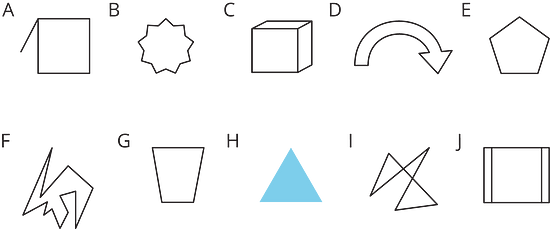
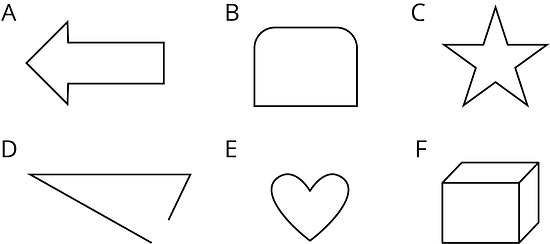
Select all the polygons.
Mark each vertex with a large dot. How many edges and vertices does this polygon have?

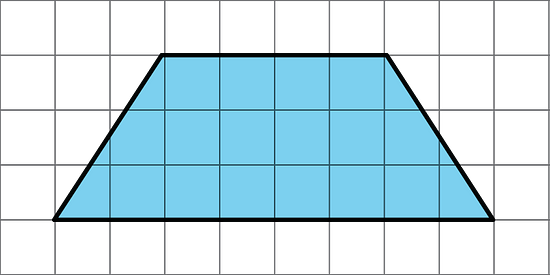
Find the area of this trapezoid. Explain or show your strategy.
Lin and Andre used different methods to find the area of a regular hexagon with 6-inch sides. Lin decomposed the hexagon into six identical triangles. Andre decomposed the hexagon into a rectangle and two triangles.
Find the area of the hexagon using each person’s method. Show your reasoning.
-
Identify a base and a corresponding height that can be used to find the area of this triangle. Label the base and the corresponding height .
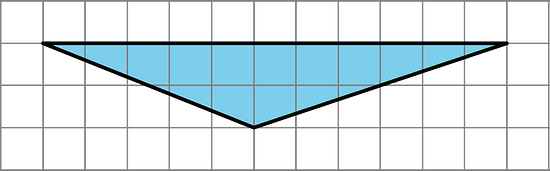
2. Find the area of the triangle. Show your reasoning.
-
On the grid, draw three different triangles with an area of 12 square units. Label the base and height of each triangle.
