Lesson 12What is Surface Area?
Let’s cover the surfaces of some three-dimensional objects.
Learning Targets:
- I know what the surface area of a three-dimensional object means.
12.1 Covering the Cabinet (Part 1)
Your teacher will show you a video about a cabinet or some pictures of it.
Estimate an answer to the question: How many sticky notes would it take to cover the cabinet, excluding the bottom?
12.2 Covering the Cabinet (Part 2)
Earlier, you learned about a cabinet being covered with sticky notes.
- How could you find the actual number of sticky notes it will take to cover the cabinet, excluding the bottom? What information would you need to know?
- Use the information you have to find the number of sticky notes needed to cover the cabinet. Show your reasoning.
Are you ready for more?
12.3 Building with Snap Cubes
Here is a rectangular prism built from 12 cubes:

It has six faces, but you can only see three of them in the sketch. It has a surface area of 32 square units.
The applet has 12 blocks, too. They are all in the same spot on the screen, like a hidden stack of blocks. You will always know where the stack is because it sits on a gray square. To use a block, drag the red point to move it. Click on the red points to change from left/right movement to up/down movement.
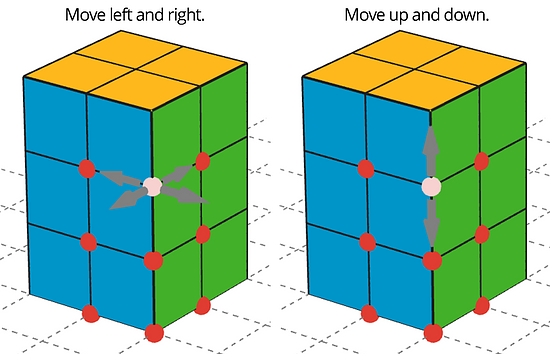
Use all 12 cubes to build a different rectangular prism (with different edge lengths than shown in the prism here). You can turn the view to see all of the faces of your figure.
- How many faces does your figure have?
- What is the surface area of your figure in square units?
Lesson 12 Summary
- The surface area of a figure (in square units) is the number of unit squares it takes to cover the entire surface without gaps or overlaps.
- If a three-dimensional figure has flat sides, the sides are called faces.
- The surface area is the total of the areas of the faces.
For example, a rectangular prism has six faces. The surface area of the prism is the total of the areas of the six rectangular faces.

So the surface area of a rectangular prism that has edge-lengths 2 cm, 3 cm, and 4 cm has a surface area of or 52 square centimeters.
Glossary Terms
Each flat side of a polyhedron is called a face. For example, a cube has 6 faces, and they are all squares.
The surface area of a polyhedron is the number of square units that covers all the faces of the polyhedron, without any gaps or overlaps.
For example, if the faces of a cube each have an area of 9 cm2, then the surface area of the cube is , or 54 cm2.
Lesson 12 Practice Problems
What is the surface area of this rectangular prism?

- 16 square units
- 32 square units
- 48 square units
- 64 square units
Which description can represent the surface area of this trunk?
- The number of square inches that cover the top of the trunk.
- The number of square feet that cover all the outside faces of the trunk.
- The number of square inches of horizontal surface inside the trunk.
- The number of cubic feet that can be packed inside the trunk.

“Trunk 1” via Wikimedia Commons. Public Domain. Which figure has a greater surface area?
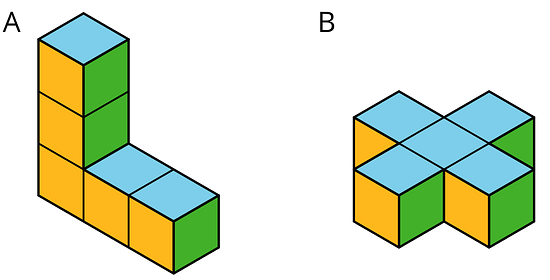
- A rectangular prism is 4 units high, 2 units wide, and 6 units long. What is its surface area in square units? Explain or show your reasoning.
Draw an example of each of the following triangles on the grid.

- A right triangle with an area of 6 square units.
- An acute triangle with an area of 6 square units.
- An obtuse triangle with an area of 6 square units.
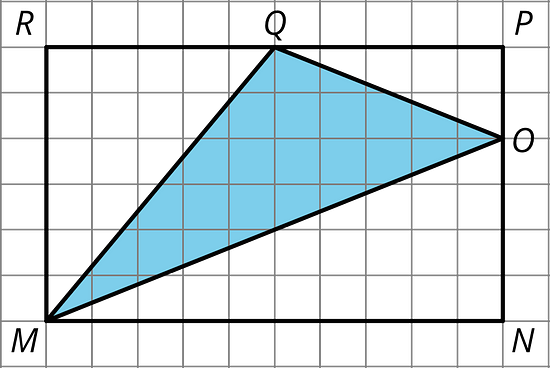
Find the area of triangle in square units. Show your reasoning.
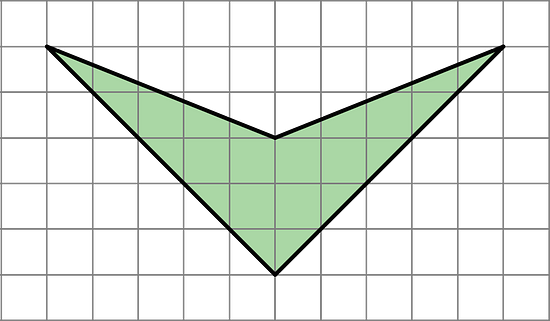
Find the area of this shape. Show your reasoning.