Open Up Resources Logo

Lesson 14Nets and Surface Area

Let’s use nets to find the surface area of polyhedra.

Learning Targets:

  • I can match polyhedra to their nets and explain how I know.
  • When given a net of a prism or a pyramid, I can calculate its surface area.

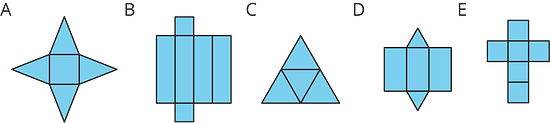
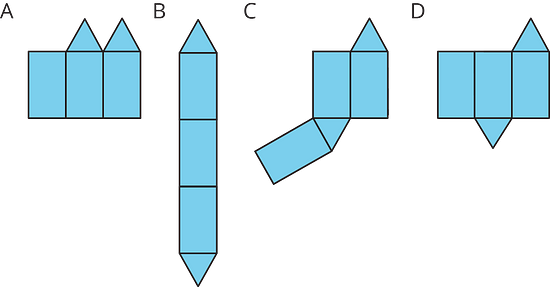
14.1 Matching Nets

Each of the following nets can be assembled into a polyhedron. Match each net with its corresponding polyhedron, and name the polyhedron. Be prepared to explain how you know the net and polyhedron go together.

Five nets of polyhedra labeled 1--5.
Five polyhedra labeled A--E.

14.2 Using Nets to Find Surface Area

Your teacher will give you the nets of three polyhedra to cut out and assemble.

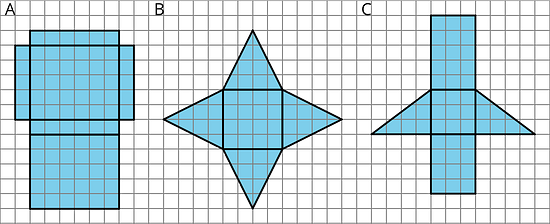
Three nets on a grid, labeled A, B, and C. Net A is composed of two rectangles that are 5 units tall by 6 units wide, two that are 5 units high and one unit wide, and two that are one unit high and six units wide. Net B is a square with a side length of 4 units and is surrounded by triangles that are four units wide at the base and four units high. Net C is a square with a side length of 3, a rectangle 3 units wide and 5 units high, another rectangle that is 3 units wide and 4 units tall, and two triangles, one on either side, that are three units tall by four units across.
  1. Name the polyhedron that each net would form when assembled.

    A:

    B:

    C:

  2. Cut out your nets and use them to create three-dimensional shapes.

  3. Find the surface area of each polyhedron. Explain your reasoning clearly.

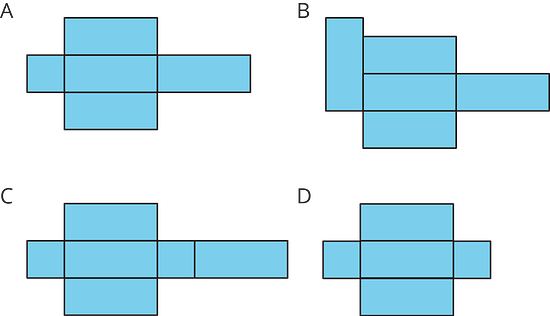
Are you ready for more?

  1. For each of these nets, decide if it can be assembled into a rectangular prism. 

    Four possible nets labeled A--D.

  2. For each of these nets, decide if it can be folded into a triangular prism. 

    Four possible nets labeled A--D.

Lesson 14 Summary

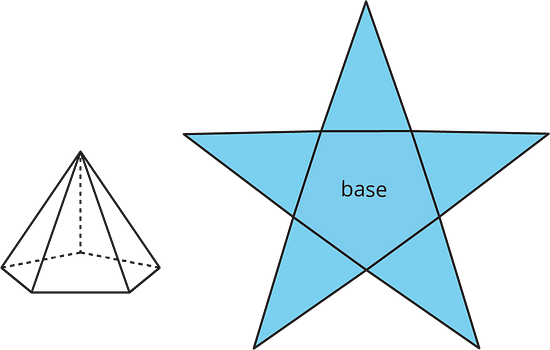
A net of a pyramid has one polygon that is the base. The rest of the polygons are triangles. A pentagonal pyramid and its net are shown here.

The net for this pentagonal pyramid is a pentagon surrounded by triangles on each side.

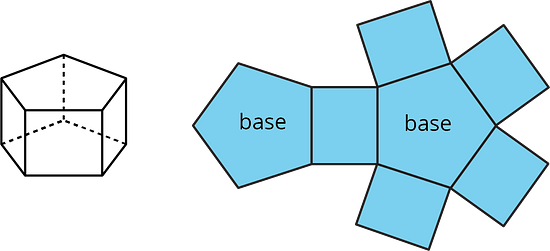
A net of a prism has two copies of the polygon that is the base. The rest of the polygons are rectangles. A pentagonal prism and its net are shown here.

The net for this pentagonal prism is a pentagon surrounded by rectangles on each side with an additional pentagon attached to the opposite side of one of the rectangles.

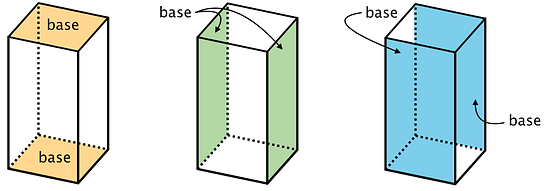
In a rectangular prism, there are three pairs of parallel and identical rectangles. Any pair of these identical rectangles can be the bases.

Three images of a rectangular prism. Each image has one set of opposing sides of the polyhedron shaded and labeled “base."
Because a net shows all the faces of a polyhedron, we can use it to find its surface area.

For instance, the net of a rectangular prism shows three pairs of rectangles: 4 units by 2 units, 3 units by 2 units, and 4 units by 3 units.

A polyhedron made up of six rectangles. Two rectangles are 8 square units in area, 2 are 6 square units, and 2 are 12 square units.

The surface area of the rectangular prism is 52 square units because 8+8+6+6+12+12=52 .

Lesson 14 Practice Problems

  1. Can the following net be assembled into a cube? Explain how you know. Label parts of the net with letters or numbers if it helps your explanation.

    A figure is composed of squares
    1. What polyhedron can be assembled from this net? Explain how you know.
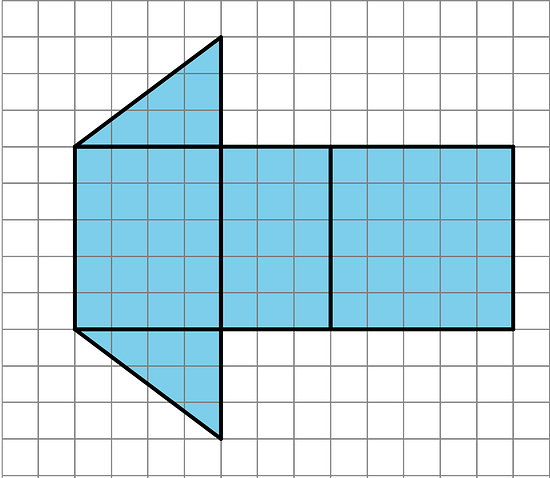
    A figure is composed of squares, triangles, and rectangles
    1. Find the surface area of this polyhedron. Show your reasoning.

  3. Here are two nets. Mai said that both nets can be assembled into the same triangular prism. Do you agree? Explain or show your reasoning.

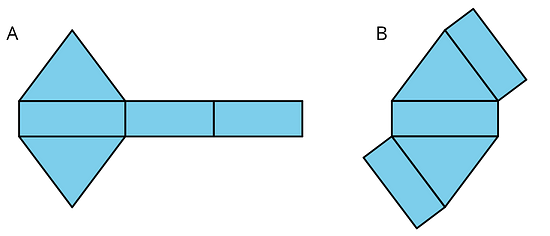
    2 figures are composed of triangles and rectangles

  4. Here are two three-dimensional figures.

    Two prisms are shown. One has a rectangle base and the other has a triangle base.

    Tell whether each of the following statements describes Figure A, Figure B, both, or neither.

    1. This figure is a polyhedron.
    2. This figure has triangular faces.
    3. There are more vertices than edges in this figure.
    4. This figure has rectangular faces.
    1. This figure is a pyramid.
    2. There is exactly one face that can be the base for this figure.
    3. The base of this figure is a triangle.
    4. This figure has two identical and parallel faces that can be the base.

  5. Select all units that can be used for surface area. Explain why the others cannot be used for surface area.

    1. square meters
    2. feet
    3. centimeters
    4. cubic inches
    5. square inches
    6. square feet

  6. Find the area of this polygon. Show your reasoning.

    An image of a 7-sided polygon. The bottom side of the polygon is six units long, and extends out to a total width of 10 units, and a central height of 6 units.