Open Up Resources Logo

Lesson 15More Nets, More Surface Area

Let’s draw nets and find the surface area of polyhedra.

Learning Targets:

  • I can calculate the surface area of prisms and pyramids.
  • I can draw the nets of prisms and pyramids.

15.1 Notice and Wonder: Wrapping Paper

Kiran is wrapping this box of sports cards as a present for a friend.

A prism with base length labeled 4 inches and base width labeled 2.5 inches.

What do you notice? What do you wonder?

15.2 Building Prisms and Pyramids

Your teacher will give you a drawing of a polyhedron. You will draw its net and calculate its surface area. 

  1. What polyhedron do you have?

  2. Study your polyhedron. Then, draw its net on graph paper. Use the side length of a grid square as the unit.

  3. Label each polygon on the net with a name or number.

  4. Find the surface area of your polyhedron. Show your thinking in an organized manner so that it can be followed by others.

When finished, pause for additional instructions from your teacher.

15.3 Comparing Boxes

Here are the nets of three cardboard boxes that are all rectangular prisms. The boxes will be packed with 1-centimeter cubes. All lengths are in centimeters.

Three nets labeled A--C.
  1. Compare the surface areas of the boxes. Which box will use the least cardboard? Show your reasoning.
  2. Now compare the volumes of these boxes in cubic centimeters. Which box will hold the most 1-centimeter cubes? Show your reasoning.

Are you ready for more?

Figure C shows a net of a cube. Draw a different net of a cube. Draw another one.  And then another one. How many different nets can be drawn and assembled into a cube?

Lesson 15 Summary

The surface area of a polyhedron is the sum of the areas of all of the faces.

Because a net shows us all faces of a polyhedron at once, it can help us find the surface area. We can find the areas of all polygons in the net and add them.

A square pyramid with a base of side length 6 and triangles of height 5.
A net with a square of side length 6 surrounded by triangles of height 5.

A square pyramid has a square and four triangles for its faces. Its surface area is the sum of the areas of the square base and the four triangular faces: (6\boldcdot 6) + 4\boldcdot \left(\frac12 \boldcdot 5 \boldcdot 6\right) = 96  The surface area of this square pyramid is 96 square units.

Lesson 15 Practice Problems

  1. Jada drew a net for a polyhedron and calculated its surface area. 

    1. What polyhedron can be assembled from this net?
    2. Jada made some mistakes in her area calculation. What were the mistakes?
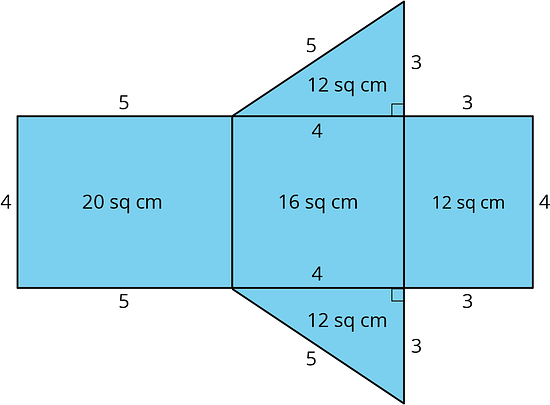
    A figure is composed of squares, triangles, and rectangles

    1. Find the surface area of the polyhedron. Show your reasoning.

  2. A cereal box is 8 inches by 2 inches by 12 inches. What is its surface area? Show your reasoning. If you get stuck, consider drawing a sketch of the box or its net and labeling the edges with their measurements.

  3. Twelve cubes are stacked to make this figure.

    A figure that looks like stairs is composed of blocks
    1. What is its surface area?
    2. How would the surface area change if the top two cubes are removed?

  4. Here are two polyhedra and their nets. Label all edges in the net with the correct lengths.

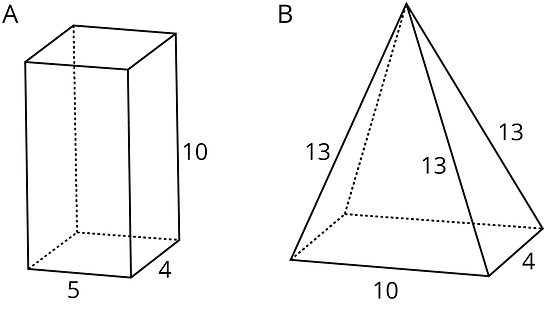
    Two polyhedra labeled A and B. Polyhedron A has sides labeled 5, 4, and 10. Polyhedron B has sides labeled 4, 10, 13, 13, and 13.
    Figure A is composed of rectangles. Figure B is composed of a rectangle and 4 traingles.
    1. What three-dimensional figure can be assembled from the net?
    a square has 4 triangles connected to its side lengths on a grid
    1. What is the surface area of the figure? (One grid square is 1 square unit.)