Lesson 7From Parallelograms to Triangles
Let’s compare parallelograms and triangles.
Learning Targets:
- I can explain the special relationship between a pair of identical triangles and a parallelogram.
7.1 Same Parallelograms, Different Bases
Here are two copies of a parallelogram. Each copy has one side labeled as the base and a segment drawn for its corresponding height and labeled .
- The base of the parallelogram on the left is 2.4 centimeters; its corresponding height is 1 centimeter. Find its area in square centimeters.
- The height of the parallelogram on the right is 2 centimeters. How long is the base of that parallelogram? Explain your reasoning.
7.2 A Tale of Two Triangles (Part 1)
Two polygons are identical if they match up exactly when placed one on top of the other.
- Draw one segment to decompose each of the following polygons into two identical triangles, if possible. If you choose to, you can also draw the triangles.
-
Which quadrilaterals can be decomposed into two identical triangles?
Pause here for a small-group discussion.
-
Study the quadrilaterals that were, in fact, decomposable into two identical triangles. What do you notice about them? Write a couple of observations about what these quadrilaterals have in common.
Are you ready for more?
Draw some other types of quadrilaterals that are not already shown. Try to decompose them into two identical triangles. Can you do it? Come up with a general rule about what must be true if a quadrilateral can be decomposed into two identical triangles.
7.3 A Tale of Two Triangles (Part 2)
This applet has eight pairs of triangles. Each group member should choose 1–2 pairs of triangles. Use them to help you answer the following questions.
- Which pair(s) of triangles do you have? _________________ Can each pair of triangles be composed into:
-
a rectangle?
-
a parallelogram?
-
- Discuss your responses to the first question with your group. Then, complete each of the following statements with all, some, or none. Sketch 1–2 examples to illustrate each completed statement.
-
________________ of these pairs of identical triangles can be composed into a rectangle.
- ________________ of these pairs of identical triangles can be composed into a parallelogram.
-
Lesson 7 Summary
A parallelogram can always be decomposed into two identical triangles by a segment that connects opposite vertices.
Going the other way around, two identical copies of a triangle can always be arranged to form a parallelogram, regardless of the type of triangle being used.
To produce a parallelogram, we can join a triangle and its copy along any of the three sides, so the same pair of triangles can make different parallelograms.
Here are examples of how two copies of both Triangle A and Triangle F can be composed into three different parallelograms.
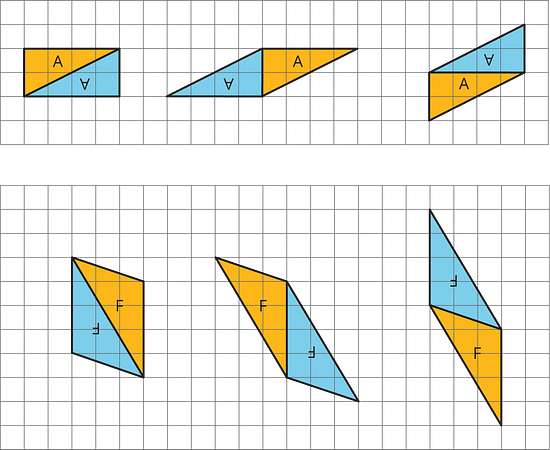
This special relationship between triangles and parallelograms can help us reason about the area of any triangle.
Lesson 7 Practice Problems
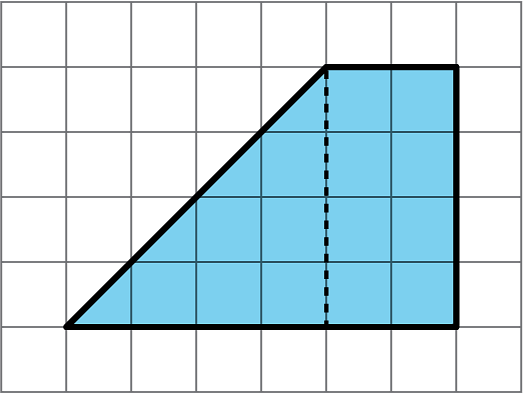
To decompose a quadrilateral into two identical shapes, Clare drew a dashed line as shown in the diagram.
-
She said the that two resulting shapes have the same area. Do you agree? Explain your reasoning.
-
Did Clare partition the figure into two identical shapes? Explain your reasoning.
-
Triangle R is a right triangle. Can we use two copies of Triangle R to compose a parallelogram that is not a square?
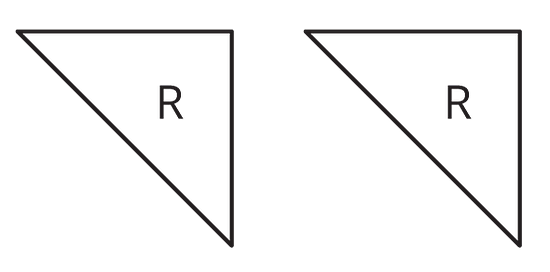
If so, explain how or sketch a solution. If not, explain why not.
Two copies of this triangle are used to compose a parallelogram. Which parallelogram cannot be a result of the composition? If you get stuck, consider using tracing paper.
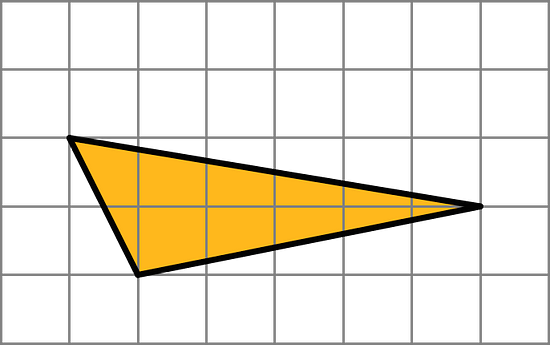

a. On the grid, draw at least three different quadrilaterals that can each be decomposed into two identical triangles with a single cut (show the cut line). One or more of the quadrilaterals should have non-right angles.

b. Identify the type of each quadrilateral.
-
A parallelogram has a base of 9 units and a corresponding height of units. What is its area?
-
A parallelogram has a base of 9 units and an area of 12 square units. What is the corresponding height for that base?
-
A parallelogram has an area of 7 square units. If the height that corresponds to a base is unit, what is the base?
-
List all segments that could represent a corresponding height if the side is the base.
