Lesson 8Area of Triangles
Let’s use what we know about parallelograms to find the area of triangles.
Learning Targets:
- I can use what I know about parallelograms to reason about the area of triangles.
8.1 Composing Parallelograms
Here is Triangle M.
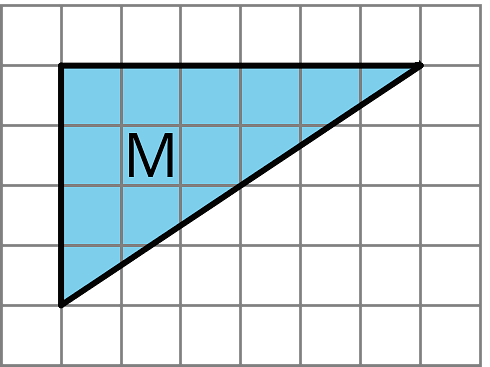
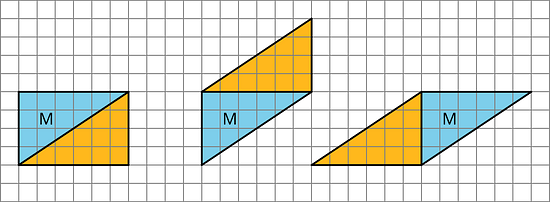
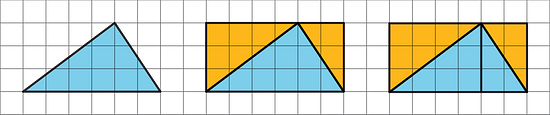
Han made a copy of Triangle M and composed three different parallelograms using the original M and the copy, as shown here.
-
For each parallelogram Han composed, identify a base and a corresponding height, and write the measurements on the drawing.
- Find the area of each parallelogram Han composed. Show your reasoning.
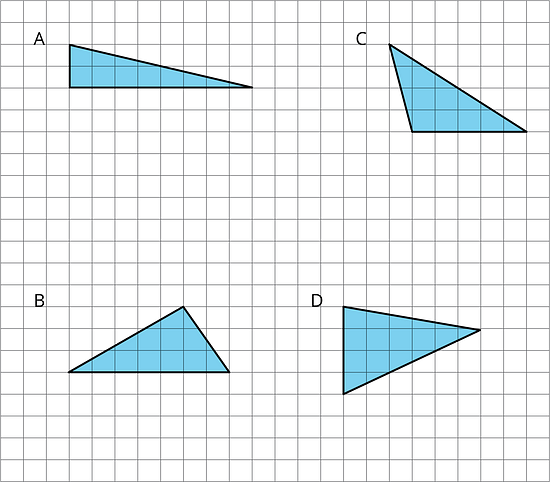
8.2 More Triangles
Find the areas of at least two of the triangles below. Show your reasoning.
8.3 Decomposing a Parallelogram
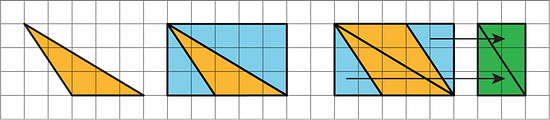
- Your teacher will give you two copies of a parallelogram. Glue or tape one copy of your parallelogram here and find its area. Show your reasoning.
- Decompose the second copy of your parallelogram by cutting along the dotted lines. Take only the small triangle and the trapezoid, and rearrange these two pieces into a different parallelogram. Glue or tape the newly composed parallelogram on your paper.
- Find the area of the new parallelogram you composed. Show your reasoning.
- What do you notice about the relationship between the area of this new parallelogram and the original one?
- How do you think the area of the large triangle compares to that of the new parallelogram: Is it larger, the same, or smaller? Why is that?
- Glue or tape the remaining large triangle below. Use any part of the work above to help you find its area. Show your reasoning.
Are you ready for more?
Can you decompose this triangle and rearrange its parts to form a rectangle? Describe how it could be done.

Lesson 8 Summary
We can reason about the area of a triangle by using what we know about parallelograms. Here are three general ways to do this:
-
Make a copy of the triangle and join the original and the copy along an edge to create a parallelogram. Because the two triangles have the same area, one copy of the triangle has half the area of that parallelogram.
The area of Parallelogram B is 16 square units because the base is 8 units and the height is 2 units. The area of Triangle A is half of that, which is 8 square units. The area of Parallelogram D is 24 square units because the base is 4 units and the height is 6 units. The area of Triangle C is half of that, which is 12 square units.
-
Decompose the triangle into smaller pieces and compose them into a parallelogram.
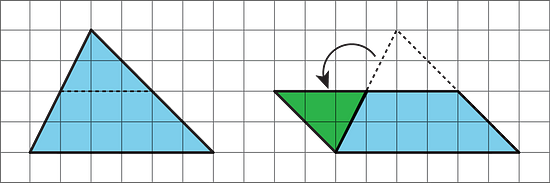
In the new parallelogram, , , and , so its area is 12 square units. Because the original triangle and the parallelogram are composed of the same parts, the area of the original triangle is also 12 square units.
-
Draw a rectangle around the triangle. The triangle has half of the area of the rectangle.
The large rectangle can be decomposed into smaller rectangles. The one on the left has area or 12 square units; the one on the right has area or 6 square units. The large triangle is also decomposed into two right triangles. Each of the right triangles is half of a smaller rectangle, so their areas are 6 square units and 3 square units. The large triangle has area 9 square units.
Sometimes, the triangle is half of what is left of the rectangle after removing two copies of the smaller right triangles.
The right triangles being removed can be composed into a small rectangle with area square units. What is left is a parallelogram with area , which equals or 9 square units. Notice that we can compose the same parallelogram with two copies of the original triangle! The original triangle is half of the parallelogram, so its area is or 4.5 square units.
Lesson 8 Practice Problems
To find the area of this right triangle, Diego and Jada used different strategies. Diego drew a line through the midpoints of the two longer sides, which decomposes the triangle into a trapezoid and a smaller triangle. He then rearranged the two shapes into a parallelogram.
Jada made a copy of the triangle, rotated it, and lined it up against one side of the original triangle so that the two triangles make a parallelogram.
- Explain how Diego might use his parallelogram to find the area of the triangle.
- Explain how Jada might use her parallelogram to find the area of the triangle.
- Find the area of the triangle. Explain or show your reasoning.a.
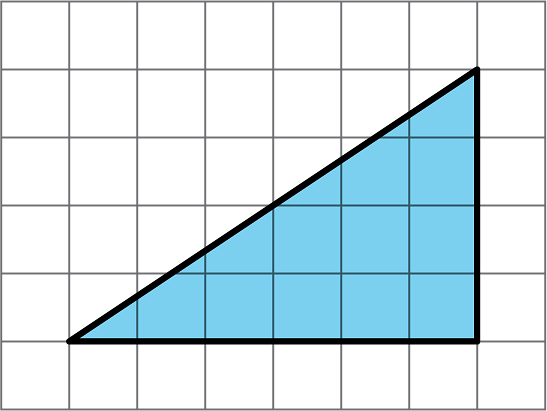 b.
b.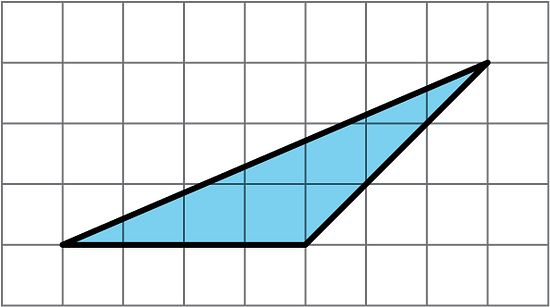
Which of the three triangles has the greatest area? Show your reasoning.
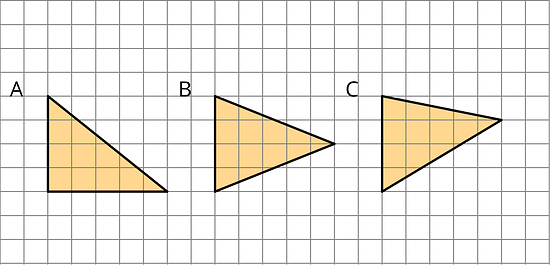
If you get stuck, use what you know about the area of parallelograms to help you.
Draw an identical copy of each triangle such that the two copies together form a parallelogram. If you get stuck, consider using tracing paper.

-
A parallelogram has a base of 3.5 units and a corresponding height of 2 units. What is its area?
-
A parallelogram has a base of 3 units and an area of 1.8 square units. What is the corresponding height for that base?
-
A parallelogram has an area of 20.4 square units. If the height that corresponds to a base is 4 units, what is the base?
-