Open Up Resources Logo

Lesson 13Rectangles with Fractional Side Lengths

Let’s explore rectangles that have fractional measurements.

Learning Targets:

  • I can use division and multiplication to solve problems involving areas of rectangles with fractional side lengths.

13.1 Areas of Squares

Three squares. The first square is labeled with side length 1 inch on the vertical side and 1 inch on the horizontal side. The second square is labeled with side length one half inch on the vertical side and one half inch on the horizontal side. The third square is labeled with side length 2 inches on the vertical side and 2 inches on the horizontal side.
  1. What do you notice about the areas of the squares? Write your observations.
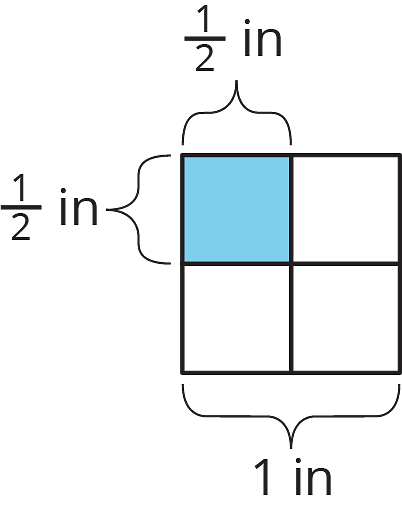
  2. Consider the statement: “A square with side lengths of \frac13 inch has an area of \frac13 square inches.” Do you agree or disagree with the statement? Explain or show your reasoning.

13.2 Areas of Squares and Rectangles

Use one piece of \frac14 -inch graph paper for the following.

  1. Use a ruler to draw a square with side length of 1 inch on the graph paper. Inside the square, draw a square with side length of \frac14 inch.

    1. How many squares with side length of  \frac 14 inch can fit in a square with side length of 1 inch?
    2. What is the area of a square with side length of  \frac 14 inch? Explain or show how you know.

  2. Use a ruler to draw a rectangle that is 3\frac12 inches by 2\frac14 inches on the graph paper. Write a division expression for each question and answer the question.

    1. How many \frac14 -inch segments are in a length of 3\frac12 inches? 
    2. How many \frac14 -inch segments are in a length of  2\frac14 inches? 
  3. Use your drawings to show that a rectangle that is  3\frac12 inches by 2\frac14 inches has an area of 7\frac 78 square inches.

13.3 Areas of Rectangles

Each of the following multiplication expressions represents the area of a rectangle.

2 \boldcdot 4

2\frac12 \boldcdot 4

2 \boldcdot 4\frac 34

2\frac12 \boldcdot 4\frac34

  1. All regions shaded in light blue have the same area. Match each diagram to the expression that you think represents its area. Be prepared to explain your reasoning.

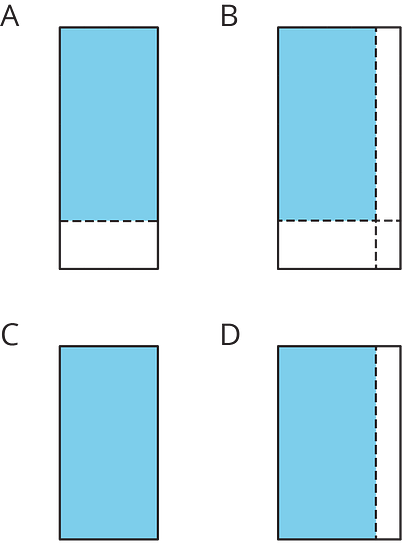
    rectangles are formed by different sized rectangles
  2. Use the diagram that matches  2\frac12 \boldcdot 4\frac34 to show that the value of  2\frac12 \boldcdot 4\frac34  is 11\frac78 .

Are you ready for more?

The following rectangles are composed of squares, and each rectangle is constructed using the previous rectangle. The side length of the first square is 1 unit.

Figures formed by different sized squares

  1. Draw the next four rectangles that are constructed in the same way. Then complete the table with the side lengths of the rectangle and the fraction of the longer side over the shorter side.

    short side long side \frac {\text {long side}}{\text{short side}}
    1
    1
    2
    3
  2. Describe the values of the fraction of the longer side over the shorter side. What happens to the fraction as the pattern continues?

13.4 How Many Would it Take? (Part 2)

Noah would like to cover a rectangular tray with rectangular tiles. The tray has a width of 11\frac14 inches and an area of 50\frac58 square inches.

  1. Find the length of the tray in inches.
  2. If the tiles are \frac{3}{4} inch by \frac{9}{16} inch, how many would Noah need to cover the tray completely, without gaps or overlaps? Explain or show your reasoning.
  3. Draw a diagram to show how Noah could lay the tiles. Your diagram should show how many tiles would be needed to cover the length and width of the tray, but does not need to show every tile.

Lesson 13 Summary

If a rectangle has side lengths a units and b units, the area is a \boldcdot b square units. For example, if we have a rectangle with  \frac12 -inch side lengths, its area is \frac12 \boldcdot \frac12 or \frac14 square inches.

A large square is divided into 4 equal squares. The large square has bottom horizontal side length labeled 1 inch. Of the four smaller squares, the top left square is shaded blue. It has side lengths labeled one half inch.

This means that if we know the area and one side length of a rectangle, we can divide to find the other side length.

A rectangle with the horizontal side labeled 10 and one half inches and the vertical side labeled with a question mark. In the center of the rectangle, 89 and one fourth square inches is indicated.

 

If one side length of a rectangle is 10\frac12 in and its area is 89\frac14 in2, we can write this equation to show their relationship:  10\frac12  \boldcdot {?} =89\frac14

Then, we can find the other side length, in inches, using division:  89\frac14 \div 10\frac12 = {?}

Lesson 13 Practice Problems

    1. Find the unknown side length of the rectangle if its area is 11 m2. Show your reasoning.
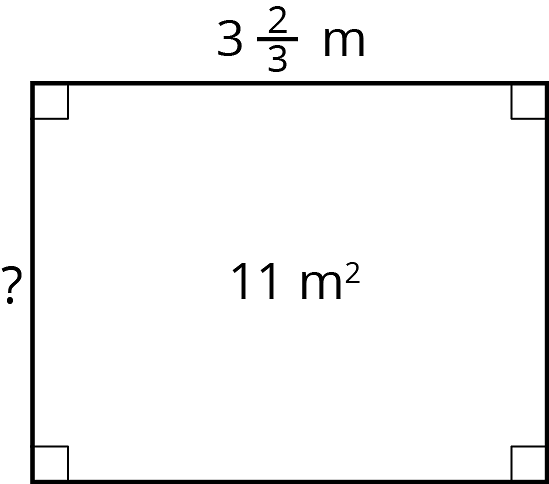
      A rectangle that is labeled 11 meters squared. The side length of one side of the rectangle is labeled "three and two thirds meters" and the side length of the other side is labeled with a question mark. Each angle is labeled with a right angle symbol.
    2. Check your answer by multiplying it by the given side length ( 3\frac 23 ). Is the resulting product 11? If not, revisit your work for the first question.

  2. A worker is tiling the floor of a rectangular room that is 12 feet by 15 feet. The tiles are square with side lengths 1\frac13 feet. How many tiles are needed to cover the entire floor? Show your reasoning.

  3. A television screen has length 16\frac12 inches, width w inches, and area 462 square inches. Select all equations that represent the relationship of the side lengths and area of the television.

    1. w \boldcdot 462 = 16\frac12
    2. 16\frac12 \boldcdot w = 462
    3. 462 \div 16\frac12 = w
    4. 462 \div w= 16\frac12
    5. 16\frac12 \boldcdot 462 = w

  4. The area of a rectangle is  17\frac12 in2 and its shorter side is 3\frac12 in. Draw a diagram that shows this information. What is the length of the longer side?

  5. A bookshelf is 42 inches long.

    1. How many books of length 1\frac12 inches will fit on the bookshelf? Explain your reasoning.
    2. A bookcase has 5 of these bookshelves. How many feet of shelf space is there? Explain your reasoning.

  6. Find the value of \frac{5}{32}\div \frac{25}{4} . Show your reasoning.

  7. How many groups of 1\frac23 are in each of the following quantities?

    a. 1\frac56

    b. 4\frac13

    c. \frac56

  8. It takes 1\frac{1}{4} minutes to fill a 3-gallon bucket of water with a hose. At this rate, how long does it take to fill a 50-gallon tub? If you get stuck, consider using the table.