Lesson 14Fractional Lengths in Triangles and Prisms
Let’s explore area and volume when fractions are involved.
Learning Targets:
- I can explain how to find the volume of a rectangular prism using cubes that have a unit fraction as their edge length.
- I can use division and multiplication to solve problems involving areas of triangles with fractional bases and heights.
- I know how to find the volume of a rectangular prism even when the edge lengths are not whole numbers.
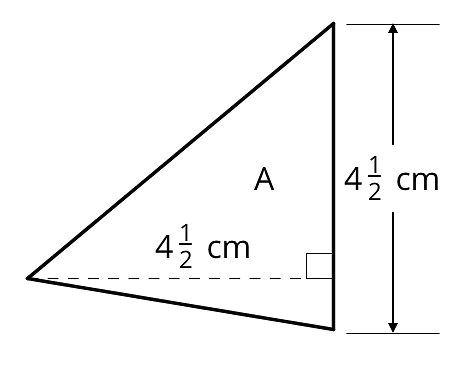
14.1 Area of Triangle
Find the area of Triangle A in square centimeters. Show your reasoning.
14.2 Bases and Heights of Triangles
- The area of Triangle B is 8 square units. Find the length of . Show your reasoning.
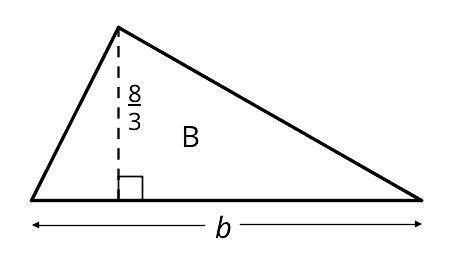
- The area of Triangle C is square units. What is the length of ? Show your reasoning.

14.3 Volumes of Cubes and Prisms
Use the cubes or the applet for the following questions.
-
Your teacher will give you a set of cubes with an edge length of inch. Use them to help you answer the following questions.
-
Here is a drawing of a cube with an edge length of 1 inch. How many cubes with an edge length of inch are needed to fill this cube?

- What is the volume, in cubic inches, of a cube with an edge length of inch? Explain or show your reasoning.
-
Four cubes are piled in a single stack to make a prism. Each cube has an edge length of inch. Sketch the prism, and find its volume in cubic inches.
-
-
Use cubes with an edge length of inch to build prisms with the lengths, widths, and heights shown in the table.
-
For each prism, record in the table how many -inch cubes can be packed into the prism and the volume of the prism.
prism
length (in)prism
width (in)prism
height (in)number of -inch
cubes in prismvolume of
prism (cu in)1 1 2 1 2 2 1 4 2 5 4 2 5 4 - Analyze the values in the table. What do you notice about the relationship between the edge lengths of each prism and its volume?
-
- What is the volume of a rectangular prism that is inches by inches by 4 inches? Show your reasoning.
Are you ready for more?
A unit fraction has a 1 in the numerator. These are unit fractions: . These are not unit fractions: .
- Find three unit fractions whose sum is . An example is: How many examples like this can you find?
- Find a box whose surface area in square units equals its volume in cubic units. How many like this can you find?
Lesson 14 Summary
If a rectangular prism has edge lengths of 2 units, 3 units, and 5 units, we can think of it as 2 layers of unit cubes, with each layer having unit cubes in it. So the volume, in cubic units, is:
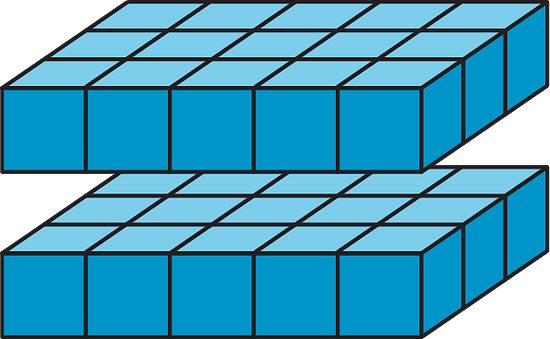
To find the volume of a rectangular prism with fractional edge lengths, we can think of it as being built of cubes that have a unit fraction for their edge length. For instance, if we build a prism that is -inch tall, -inch wide, and 4 inches long using cubes with a -inch edge length, we would have:
- A height of 1 cube, because
- A width of 3 cubes, because
- A length of 8 cubes, because
The volume of the prism would be , or 24 cubic units. How do we find its volume in cubic inches?
We know that each cube with a -inch edge length has a volume of cubic inch, because . Since the prism is built using 24 of these cubes, its volume, in cubic inches, would then be , or 3 cubic inches.
The volume of the prism, in cubic inches, can also be found by multiplying the fractional edge lengths in inches:
Lesson 14 Practice Problems
Clare is using little wooden cubes with edge length inch to build a larger cube that has edge length 4 inches. How many little cubes does she need? Explain your reasoning.
The triangle has an area of cm2 and a base of cm.
What is the length of ? Explain your reasoning.
-
Which of the following expressions can be used to find how many cubes with edge length of unit fit in a prism that is 5 units by 5 units by 8 units? Explain or show your reasoning.
-
-
Mai says that we can also find the answer by multiplying the edge lengths of the prism and then multiplying the result by 27. Do you agree with her statement? Explain your reasoning.
-
A builder is building a fence with -inch-wide wooden boards, arranged side-by-side with no gaps. How many boards are needed to build a fence that is 150 inches long? Show your reasoning.
Find the value of each expression. Show your reasoning and check your answer.
A bucket contains gallons of water and is full. How many gallons of water would be in a full bucket?
Write a multiplication and a division equation to represent the situation, and then find the answer. Show your reasoning.
There are 80 kids in a gym. 75% are wearing socks. How many are not wearing socks? If you get stuck, consider using a tape diagram showing sections that each represent 25% of the kids in the gym.
- Lin wants to save $75 for a trip to the city. If she has saved $37.50 so far, what percentage of her goal has she saved? What percentage remains?
- Noah wants to save $60 so that he can purchase a concert ticket. If he has saved $45 so far, what percentage of his goal has he saved? What percentage remains?