Lesson 9Using the Partial Quotients Method
Let’s divide whole numbers.
Learning Targets:
- I can use the partial quotients method to find a quotient of two whole numbers when the quotient is a whole number.
9.1 Using Base-Ten Diagrams to Calculate Quotients
Elena used base-ten diagrams to find . She started by representing 372.
She made 3 groups, each with 1 hundred. Then, she put the tens and ones in each of the 3 groups. Here is her diagram for .
Discuss with a partner:
- Elena’s diagram for 372 has 7 tens. The one for has only 6 tens. Why?
- Where did the extra ones (small squares) come from?
9.2 Using the Partial Quotients Method to Calculate Quotients
-
Andre calculated using a method that was different from Elena’s.
Discuss the following questions with a partner:
- Andre subtracted 600 from 657. What does the 600 represent?
- Andre wrote 10 above the 200, and then subtracted 30 from 57. How is the 30 related to the 10?
- What do the numbers 200, 10, and 9 represent?
- What is the meaning of the 0 at the bottom of Andre’s work?
-
How might Andre calculate ? Explain or show your reasoning.
9.3 What’s the Quotient?
- Find the quotient of using one of the methods you have seen so far. Show your reasoning.
-
Find each quotient and show your reasoning. Use the partial quotients method at least once.
Lesson 9 Summary
We can find the quotient in different ways.
One way is to use a base-ten diagram to represent the hundreds, tens, and ones and to create equal-sized groups.
We can think of the division by 3 as splitting up 345 into 3 equal groups.
Another way to divide 345 by 3 is by using the partial quotients method, in which we keep subtracting 3 groups of some amount from 345.
- In the calculation on the left, first we subtract 3 groups of 100, then 3 groups of 10, and then 3 groups of 5. Adding up the partial quotients () gives us 115.
- The calculation on the right shows a different amount per group subtracted each time (3 groups of 15, 3 groups of 50, and 3 more groups of 50), but the total amount in each of the 3 groups is still 115. There are other ways of calculating using the partial quotients method.
Both the base-ten diagrams and partial quotients methods are effective. If, however, the dividend and divisor are large, as in , then the base-ten diagrams will be time-consuming.
Lesson 9 Practice Problems
Here is one way to find using partial quotients.
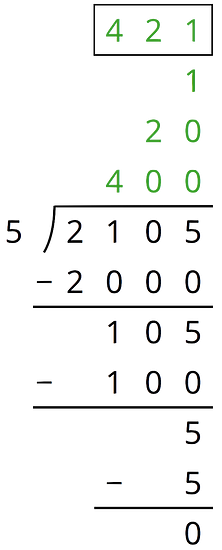
Show a different way of using partial quotients to divide 2,105 by 5.
- Andre and Jada both found using the partial quotients method, but they did the calculations differently, as shown here.
- How is Jada's work similar to and different from Andre’s work?
- Explain why they have the same answer.
- Which might be a better way to evaluate : drawing base-ten diagrams or using the partial quotients method? Explain your reasoning.
Here is an incomplete calculation of .
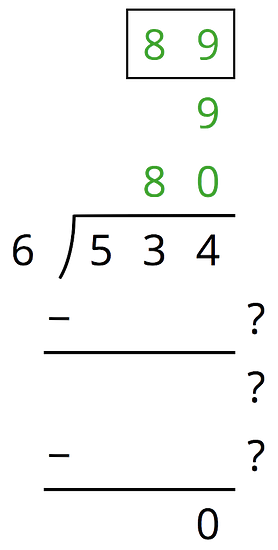
Write the missing numbers (marked with “?”) that would make the calculation complete.
Use the partial quotients method to find .
Which of the polygons has the greatest area?
- A rectangle that is 3.25 inches wide and 6.1 inches long.
- A square with side length of 4.6 inches.
- A parallelogram with a base of 5.875 inches and a height of 3.5 inches.
- A triangle with a base of 7.18 inches and a height of 5.4 inches.
One micrometer is a millionth of a meter. A certain spider web is 4 micrometers thick. A fiber in a shirt is 1 hundred-thousandth of a meter thick.
- Which is wider, the spider web or the fiber? Explain your reasoning.
- How many meters wider?