Lesson 2Corresponding Parts and Scale Factors

Let’s describe features of scaled copies.

Learning Targets:

I can describe what the scale factor has to do with a figure and its scaled copy.
In a pair of figures, I can identify corresponding points, corresponding segments, and corresponding angles.

2.1 Number Talk: Multiplying by a Unit Fraction

Find each product mentally.

2.2 Corresponding Parts

One road sign for railroad crossings is a circle with a large X in the middle and two R’s—with one on each side. Here is a picture with some points labeled and two copies of the picture. Drag and turn the moveable angle tool to compare the angles in the copies with the angles in the original.

open applet in presentation mode

Complete this table to show corresponding parts in the three pictures.

original	Copy 1	Copy 2
point
segment
	segment
		point
angle
		angle

Is either copy a scaled copy of the original road sign? Explain your reasoning.
Use the moveable angle tool to compare angle with its corresponding angles in Copy 1 and Copy 2. What do you notice?
Use the moveable angle tool to compare angle with its corresponding angles in Copy 1 and Copy 2. What do you notice?

2.3 Scaled Triangles

Here is Triangle O, followed by a number of other triangles.

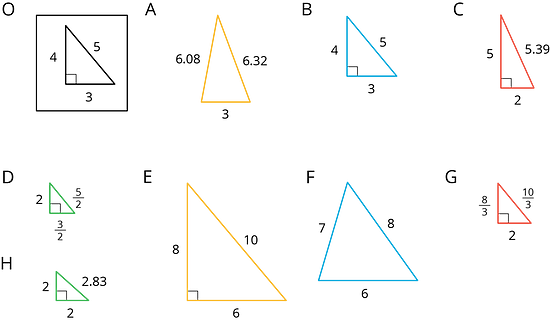
Right triangle O, has sides 3, 4, 5. Right triangle A has sides 2, 3 halves, 5 halves. B has sides 6.08 and 6.32. C has sides 6, 7, 8. Right triangle D has sides 2, 5, and 5.39. Right triangle E has sides 2, 2, and 2.38. Right triangle F has sides 6, 8, and 10. Right triangle G has sides 3, 4, and 5. Right triangle H has sides 2, 8 thirds, and 10 thirds.

Your teacher will assign you two of the triangles to look at.

For each of your assigned triangles, is it a scaled copy of Triangle O? Be prepared to explain your reasoning.
As a group, identify all the scaled copies of Triangle O in the collection. Discuss your thinking. If you disagree, work to reach an agreement.

List all the triangles that are scaled copies in the table. Record the side lengths that correspond to the side lengths of Triangle O listed in each column.

Triangle O	3	4	5

Explain or show how each copy has been scaled from the original (Triangle O).

Are you ready for more?

Choose one of the triangles that is not a scaled copy of Triangle O. Describe how you could change at least one side to make a scaled copy, while leaving at least one side unchanged.

Lesson 2 Summary

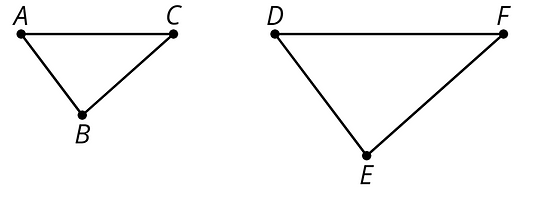
A figure and its scaled copy have corresponding parts, or parts that are in the same position in relation to the rest of each figure. These parts could be points, segments, or angles. For example, Polygon 2 is a scaled copy of Polygon 1.

Polygon 1 is A, F, E, D, C, B with side lengths, 2.8, 2, 1.3, 2, 3.2, and 3. Polygon 2 is G, L, K, J, I, H with side lengths 5.6, 4, 2.6, 4, 6.4, and 6.

Each point in Polygon 1 has a corresponding point in Polygon 2.
For example, point corresponds to point and point corresponds to point .
Each segment in Polygon 1 has a corresponding segment in Polygon 2.
For example, segment corresponds to segment .
Each angle in Polygon 1 also has a corresponding angle in Polygon 2.
For example, angle corresponds to angle .

The scale factor between Polygon 1 and Polygon 2 is 2, because all of the lengths in Polygon 2 are 2 times the corresponding lengths in Polygon 1. The angle measures in Polygon 2 are the same as the corresponding angle measures in Polygon 1: for example, the measure of angle is the same as the measure of angle .

Glossary Terms

corresponding

When part of an original figure matches up with part of a copy, we call them corresponding parts. These could be points, segments, angles, or distances.

For example, point in the first triangle corresponds to point in the second triangle.

Segment corresponds to segment .

Corresponding triangles ABC and DEF are shown.

scale factor

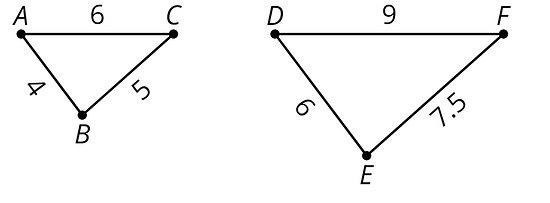
To create a scaled copy, we multiply all the lengths in the original figure by the same number. This number is called the scale factor.

In this example, the scale factor is 1.5, because , , and .

Two similar triangles are shown. One is smaller than the other.

Lesson 2 Practice Problems

The second H-shaped polygon is a scaled copy of the first.
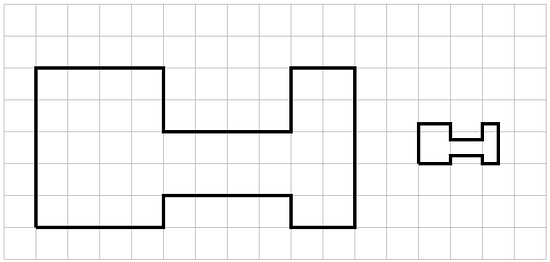
1. Show one pair of corresponding points and two pairs of corresponding sides in the original polygon and its copy. Consider using colored pencils to highlight corresponding parts or labeling some of the vertices.
2. What scale factor takes the original polygon to its smaller copy? Explain or show your reasoning.
Figure B is a scaled copy of Figure A. Select all of the statements that must be true:
1. Figure B is larger than Figure A.
2. Figure B has the same number of edges as Figure A.
3. Figure B has the same perimeter as Figure A.
4. Figure B has the same number of angles as Figure A.
5. Figure B has angles with the same measures as Figure A.
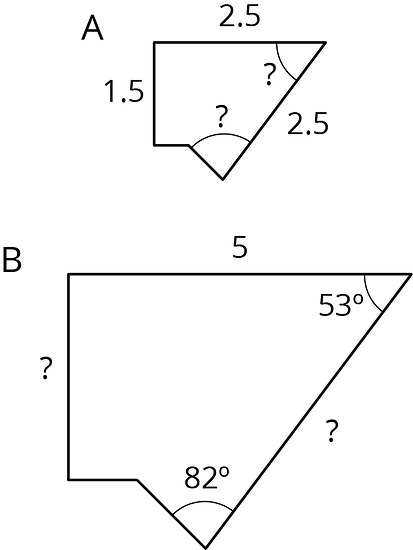
Polygon B is a scaled copy of Polygon A.
What is the scale factor from Polygon A to Polygon B? Explain your reasoning.

Find the missing length of each side marked with ? in Polygon B.

Determine the measure of each angle marked with ? in Polygon A.
Complete each equation with a number that makes it true.