Open Up Resources Logo

Lesson 3Making Scaled Copies

Let’s draw scaled copies.

Learning Targets:

  • I can draw a scaled copy of a figure using a given scale factor.
  • I know what operation to use on the side lengths of a figure to produce a scaled copy.

3.1 More or Less?

For each problem, select the answer from the two choices.

  1. The value of 25\boldcdot (8.5) is:
    1. More than 205
    2. Less than 205
  2. The value of (9.93)\boldcdot (0.984) is:
    1. More than 10
    2. Less than 10
  3. The value of (0.24)\boldcdot (0.67) is:
    1. More than 0.2
    2. Less than 0.2

3.2 Drawing Scaled Copies

Figure A is a quadrilateral with side lengths 2, 3, 3, and diagonal side up 3 over 1 units. Figure C is a 6 by 3 rectangle with a 2 by 4 rectangle appended to the left top 2 squares and a 1 by 2 rectangle appended to the top right square.
  1. Draw a scaled copy of either Figure A or B using a scale factor of 3.
  2. Draw a scaled copy of either Figure C or D using a scale factor of \frac12 .
open applet in presentation mode

3.3 Which Operations? (Part 1)

Diego and Jada want to scale this polygon so the side that corresponds to 15 units in the original is 5 units in the scaled copy.

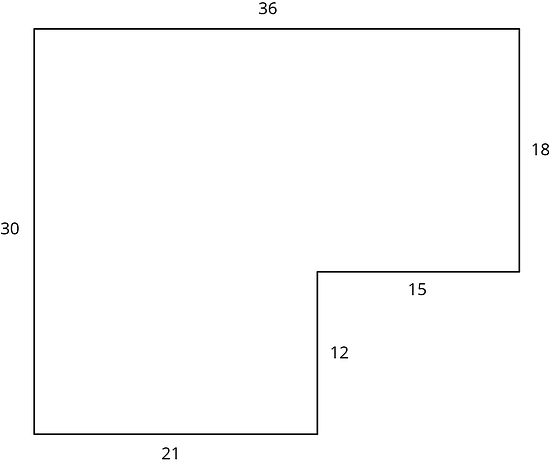
Original polygon is a rectangle of height 30 and length 36 with a rectangle of height 12 and length 15 removed from the bottom right corner.

Diego and Jada each use a different operation to find the new side lengths. Here are their finished drawings.

Diego's drawing has 6 side lengths of 26, 8, 5, 2, 11, and 20, but the sides do not connect to form a closed figure. Jada's drawing is a rectangle of height 10 and length 12 with a rectangle of height 4, length 5 removed from the bottom right corner.
  1. What operation do you think Diego used to calculate the lengths for his drawing?
  2. What operation do you think Jada used to calculate the lengths for her drawing?
  3. Did each method produce a scaled copy of the polygon? Explain your reasoning.

3.4 Which Operations? (Part 2)

Andre wants to make a scaled copy of Jada's drawing so the side that corresponds to 4 units in Jada’s polygon is 8 units in his scaled copy.

  1. Andre says “I wonder if I should add 4 units to the lengths of all of the segments?” What would you say in response to Andre? Explain or show your reasoning.

  2. Create the scaled copy that Andre wants. If you get stuck, consider using the edge of an index card or paper to measure the lengths needed to draw the copy.
A polygon with side lengths 12, 6, 5, 4, 7, and 10.

Are you ready for more?

The side lengths of Triangle B are all 5 more than the side lengths of Triangle A. Can Triangle B be a scaled copy of Triangle A? Explain your reasoning.

Lesson 3 Summary

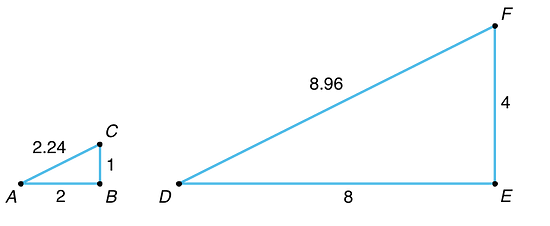
Creating a scaled copy involves multiplying the lengths in the original figure by a scale factor.

For example, to make a scaled copy of triangle ABC where the base is 8 units, we would use a scale factor of 4. This means multiplying all the side lengths by 4, so in triangle DEF , each side is 4 times as long as the corresponding side in triangle ABC .

Triangle A, B, C has side lengths 2, 1, and 2.24. Triangle D, E, F has side lengths 8, 4, and 8.96.

Lesson 3 Practice Problems

  1. Here are 3 polygons.

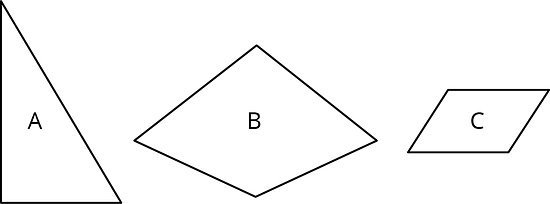
    Three polygons labeled A, B, and C. Figure A is a right, scalene triangle resting on its horizontal shorter leg. Figure B is a quadrilateral with two pairs of sides of equal lengths. The shorter sides make a V shape and the longer sides make an upside-down V shape. Figure C is a parallelogram resting on one of its longer sides, tilted to the right.

    Draw a scaled copy of Polygon A using a scale factor of 2.

    Draw a scaled copy of Polygon B using a scale factor of \frac{1}{2} .

    Draw a scaled copy of Polygon C using a scale factor of \frac{3}{2} .

  2. Quadrilateral A has side lengths 6, 9, 9, and 12. Quadrilateral B is a scaled copy of Quadrilateral A, with its shortest side of length 2. What is the perimeter of Quadrilateral B?

  3. Here is a polygon on a grid.

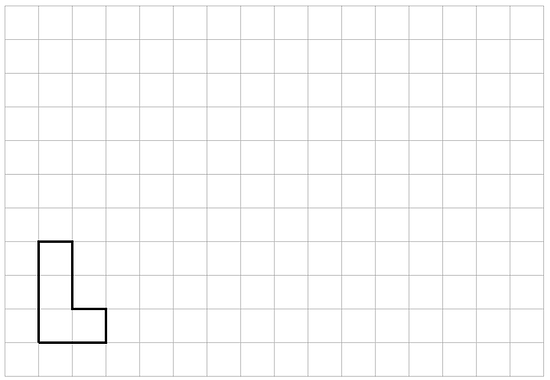
    An L shaped figure on a square grid. The polygon is composed of two shapes: a rectangle adjoined with a square so that the bottom horizontal base of the polygon is 2 units. The rectangle is 1 unit wide and 3 units in length. The square is 1 unit wide and 1 unit in length.

    Draw a scaled copy of this polygon that has a perimeter of 30 units. What is the scale factor? Explain how you know.

  4. Priya and Tyler are discussing the figures shown below. Priya thinks that B, C, and D are scaled copies of A. Tyler says B and D are scaled copies of A. Do you agree with Priya, or do you agree with Tyler? Explain your reasoning.

    Four shapes that look like plus signs. Shape A is one square with a square appended to each side. Shape B is one square with a 1 by 2 rectangle appended to each side. Shape C is a 2 by 2 square with a 1 by 2 rectangle appended to each side. Shape D is a 2 by 2 square with a 2 by 2 square appended to each side.