Open Up Resources Logo

Lesson 4Scaled Relationships

Let’s find relationships between scaled copies.

Learning Targets:

  • I can use corresponding distances and corresponding angles to tell whether one figure is a scaled copy of another.
  • When I see a figure and its scaled copy, I can explain what is true about corresponding angles.
  • When I see a figure and its scaled copy, I can explain what is true about corresponding distances.

4.1 Three Quadrilaterals (Part 1)

Each of these polygons is a scaled copy of the others.

Polygon A, B, C, D. Polygon E, F, G, H. Polygon I, J, K, L.
  1. Name two pairs of corresponding angles. What can you say about the sizes of these angles?
  2. Check your prediction by measuring at least one pair of corresponding angles using a protractor. Record your measurements to the nearest 5^\circ .

4.2 Three Quadrilaterals (Part 2)

Each of these polygons is a scaled copy of the others. You already checked their corresponding angles.

Polygon A, B, C, D. Polygon E, F, G, H. Polygon I, J, K, L.
  1. The side lengths of the polygons are hard to tell from the grid, but there are other corresponding distances that are easier to compare. Identify the distances in the other two polygons that correspond to DB and AC , and record them in the table.
    quadrilateral distance that
    corresponds to DB     		distance that
    corresponds to AC
    ABCD DB = 4 AC = 6
    EFGH
    IJKL

  2. Look at the values in the table. What do you notice?

    Pause here so your teacher can review your work.

  3. The larger figure is a scaled copy of the smaller figure.

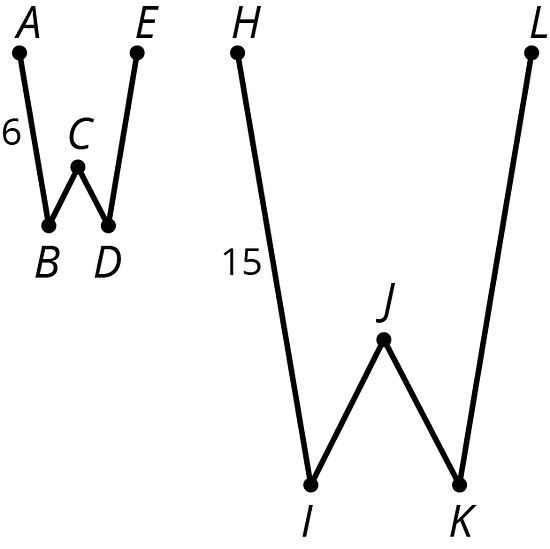
    Both figures resemble the letter W. Tracing each, the smaller figure's vertices in order are A, B, C, D, E. The length of segment A, B is 6. The larger W is H, I, J, K, L. The length of segment H, I is 15.
    1. If AE = 4 , how long is the corresponding distance in the second figure? Explain or show your reasoning.
    2. If IK = 5 , how long is the corresponding distance in the first figure? Explain or show your reasoning.

4.3 Scaled or Not Scaled?

Here are two quadrilaterals.

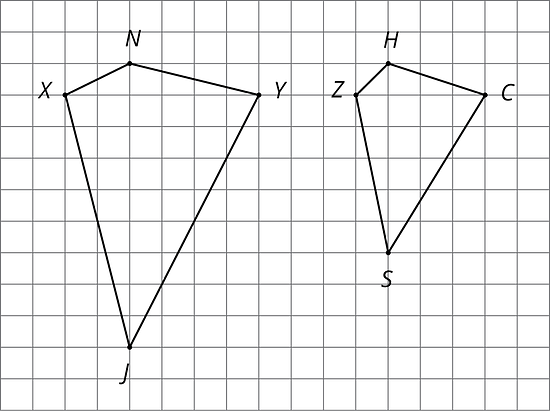
Two quadrilaterals on a coordinate plane. The first figure is labeled JXNY. Point X is 2 units to the left and 8 units up from point J. Point N is 2 units to the right and 1 unit up from point X. Point Y is 4 units to the right and 1 unit down from point N. Point J is 4 units to the left and 8 units down from point Y. Point N is directly above point J. The second figure is labeled ZHCS. Point Z is 1 unit to the left and 5 units up from point S. Point H is 1 unit to the right and 1 unit up from point Z. Point C is 3 units to the right and 1 unit down from point H. Point S is 3 units to the left and 5 units down from point C. Point H is directly above point S.
  1. Mai says that Polygon ZSCH is a scaled copy of Polygon XJYN , but Noah disagrees. Do you agree with either of them? Explain or show your reasoning.
  2. Record the corresponding distances in the table. What do you notice?
    quadrilateral horizontal distance vertical distance
    XJYN XY = \phantom{33} JN = \phantom{33}
    ZSCH ZC = \phantom{33} SH = \phantom{33}
  3. Measure at least three pairs of corresponding angles in XJYN and ZSCH using a protractor. Record your measurements to the nearest 5^\circ . What do you notice?
  4. Do these results change your answer to the first question? Explain.

Here are two more quadrilaterals.

The angle measures, in degrees, for both trapezoids are: 60, 60, 120, 120. In A, B, C, D, the top length is 2, bottom length is 6, both sides lengths are 4. In E, F, G, H, the top length is 1, bottom length is 4 and both side lengths are 3.
  1. Kiran says that Polygon EFGH is a scaled copy of ABCD , but Lin disagrees. Do you agree with either of them? Explain or show your reasoning.

Are you ready for more?

All side lengths of quadrilateral MNOP are 2, and all side lengths of quadrilateral QRST are 3. Does MNOP have to be a scaled copy of QRST ? Explain your reasoning.

4.4 Comparing Pictures of Birds

Here are two pictures of a bird. Find evidence that one picture is not a scaled copy of the other. Be prepared to explain your reasoning.

open applet in presentation mode

Lesson 4 Summary

When a figure is a scaled copy of another figure, we know that:

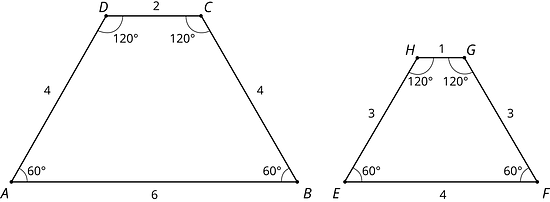
  1. All distances in the copy can be found by multiplying the corresponding distances in the original figure by the same scale factor, whether or not the endpoints are connected by a segment.

    For example, Polygon STUVWX is a scaled copy of Polygon ABCDEF . The scale factor is 3. The distance from T to X is 6, which is three times the distance from B to F .

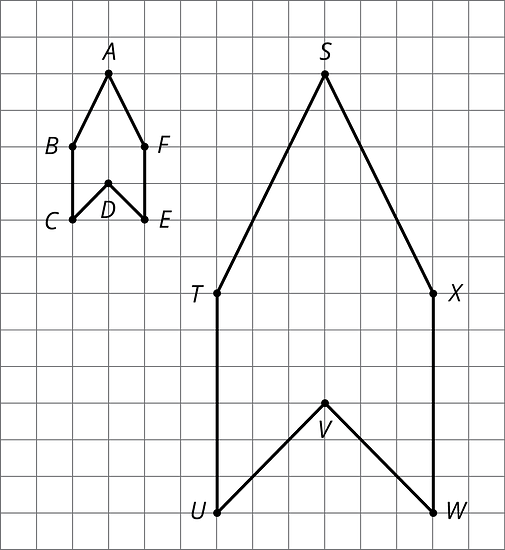
Two similar figures on a grid
  1. All angles in the copy have the same measure as the corresponding angles in the original figure, as in these triangles.
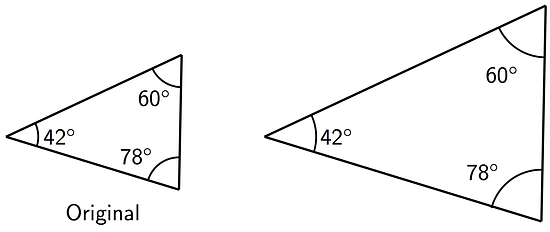
Original triangle has angle measures 42, 60, and 78 degrees. The larger, scaled version of the triangle has angle measures 42, 60, and 78 degrees.

These observations can help explain why one figure is not a scaled copy of another.

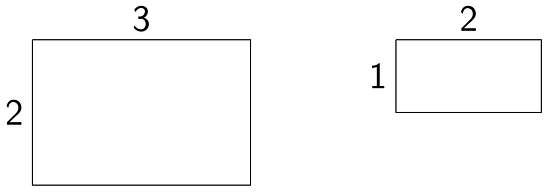
For example, even though their corresponding angles have the same measure, the second rectangle is not a scaled copy of the first rectangle, because different pairs of corresponding lengths have different scale factors,  2 \boldcdot \frac12 = 1 but 3 \boldcdot \frac23 = 2 .

The first rectangle has height 2 and length 3. The second rectangle has height 1 and length 2.

Lesson 4 Practice Problems

  1. Select all the statements that must be true for any scaled copy Q of Polygon P.

    Angle measures of Polygon P clockwise from bottom left, in degrees, 90, 125, 35, 250, 80, 135.

    1. The side lengths are all whole numbers.

    2. The angle measures are all whole numbers.

    3. Q has exactly 1 right angle.

    4. If the scale factor between P and Q is \frac15 , then each side length of P is multiplied by \frac15 to get the corresponding side length of Q.

    5. If the scale factor is 2, each angle in P is multiplied by 2 to get the corresponding angle in Q.

    6. Q has 2 acute angles and 3 obtuse angles.

  2. Here is Quadrilateral ABCD .

    Quadrilateral ABCD is on a grid. Point a is 2 units right and 4 units down from the edge of the grid. Point B is 2 units right and 2 units up from point A. Point C is 6 units right from point A. Point D is 2 units right and 4 units down from point A.

    Quadrilateral PQRS is a scaled copy of Quadrilateral ABCD . Point  P corresponds to A , Q to B , R to C , and S to D .

    If the distance from P to R is 3 units, what is the distance from  Q to S ? Explain your reasoning.

  3. Figure 2 is a scaled copy of Figure 1.

    Two 4-sided figures in a coordinate plane labeled Figure 1 and Figure 2. Figure 1 has four points. Point A is 3 units to the left and 2 units up from the bottom-right point. The top-right point is 1 unit up and 3 units to the right of point A. Point C is 1 unit down and 1 unit to the left of the top-right point. The bottom-right point is 1 unit to the right and 2 units down from point C. The bottom-right point is directly below the top-right point. Lines are drawn connecting point A to the top-right point, the top-right to C, C to the bottom-right point, and the bottom-right to A. Figure 2 also has four points. The left-most point is 9 units to the left and 6 units up from point S. Point Q is 3 units up and 9 units to the right of the left-most point. A fourth point is 3 units down and 3 units to the left of point Q. Point S is 3 units to the right and 6 units down from the fourth point. Point S is directly below point Q. Lines are drawn connecting the left-most point to Q, Q to the fourth point, the fourth point to S, and S to the left-most point.
    1. Identify the points in Figure 2 that correspond to the points A and C in Figure 1. Label them P and R . What is the distance between P and R ?
    2. Identify the points in Figure 1 that correspond to the points Q and S in Figure 2. Label them B and D . What is the distance between B and D ?
    3. What is the scale factor that takes Figure 1 to Figure 2?
    4. G and H are two points on Figure 1, but they are not shown. The distance between G and H is 1. What is the distance between the corresponding points on Figure 2?

  4. To make 1 batch of lavender paint, the ratio of cups of pink paint to cups of blue paint is 6 to 5. Find two more ratios of cups of pink paint to cups of blue paint that are equivalent to this ratio.