Open Up Resources Logo

Lesson 3Exploring Circumference

Let’s explore the circumference of circles.

Learning Targets:

  • I can describe the relationship between circumference and diameter of any circle.
  • I can explain what \pi means.

3.1 Which Is Greater?

Clare wonders if the height of the toilet paper tube or the distance around the tube is greater. What information would she need in order to solve the problem? How could she find this out?

Three different views of a circular shaped toilet paper tube. The first view is of the vertical height of the tube. The second view is of the circular base of the tube. The third view is of both the base and the height of the tube.

3.2 Measuring Circumference and Diameter

Coins, cookies, and drinking glasses are some examples of common circular objects.

  1. Explore the applet to find the diameter and the circumference of three circular objects to the nearest tenth of a unit. Record your measurements in the table. 

    open applet in presentation mode

  1. Plot the diameter and circumference values from the table on the coordinate plane. What do you notice?

    open applet in presentation mode
  1. Plot the points from two other groups on the same coordinate plane. Do you see the same pattern that you noticed earlier?

Are you ready for more?

Suppose you had another circular object with a diameter that is half as long as the diameter of your largest circle. What would its circumference be?

3.3 Calculating Circumference and Diameter

Here are five circles. One measurement for each circle is given in the table.

Five circles, each with a different diameter, are labeled A, B, C, D, and E.

Use the constant of proportionality estimated in the previous activity to complete the table.

diameter (cm) circumference (cm)
circle A 3
circle B 10
circle C 24
circle D 18
circle E 1

Are you ready for more?

The circumference of the Earth is approximately 40,000 km. If you made a circle of wire around the globe, that is only 10 meters (0.01 km) longer than the circumference of the globe, could a flea, a mouse, or even a person creep under it?

Lesson 3 Summary

There is a proportional relationship between the diameter and circumference of any circle. That means that if we write C for circumference and d for diameter, we know that C=kd , where k is the constant of proportionality.

The exact value for the constant of proportionality is called \boldsymbol\pi . Some frequently used approximations for \pi are \frac{22} 7 , 3.14, and 3.14159, but none of these is exactly \pi .

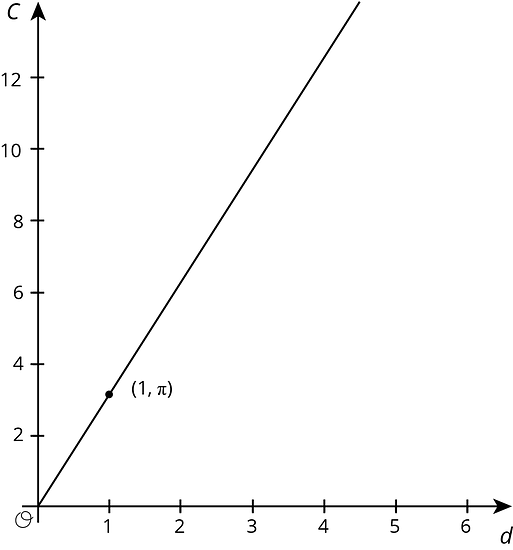
A graph of a line in the coordinate plane with the origin labeled O. The horizontal axis is labeled “d” and the numbers 1 through 6 are indicated. The vertical axis is labeled “C” and the numbers 2 through 12, in increments of 2, are indicated. The line begins at the origin, slants upward and to the right, and passes through the point 1 comma pi.

We can use this to estimate the circumference if we know the diameter, and vice versa. For example, using 3.1 as an approximation for \pi , if a circle has a diameter of 4 cm, then the circumference is about (3.1)\boldcdot 4 = 12.4 or 12.4 cm.

The relationship between the circumference and the diameter can be written as

C = \pi d

Glossary Terms

pi ( \pi )

There is a proportional relationship between the diameter and circumference of any circle. The constant of proportionality is pi. The symbol for pi is \pi . 

We can represent this relationship with the equation C = \pi d , where C represents the circumference and d represents the diameter.

Some approximations for \pi are \frac{22}{7} , 3.14, and 3.14159.

A graph of a line in the coordinate plane with the origin labeled O. The horizontal axis is labeled “d” and the numbers 1 through 6 are indicated. The vertical axis is labeled “C” and the numbers 2 through 12, in increments of 2, are indicated. The line begins at the origin, slants upward and to the right, and passes through the point 1 comma pi.

Lesson 3 Practice Problems

  1. Diego measured the diameter and circumference of several circular objects and recorded his measurements in the table.

    object diameter (cm) circumference (cm)
    half dollar coin 3 10
    flying disc 23 28
    jar lid 8 25
    flower pot 15 48

    One of his measurements is inaccurate. Which measurement is it? Explain how you know.

  2. Complete the table. Use one of the approximate values for \pi discussed in class (for example 3.14, \frac{22}{7} , 3.1416). Explain or show your reasoning.

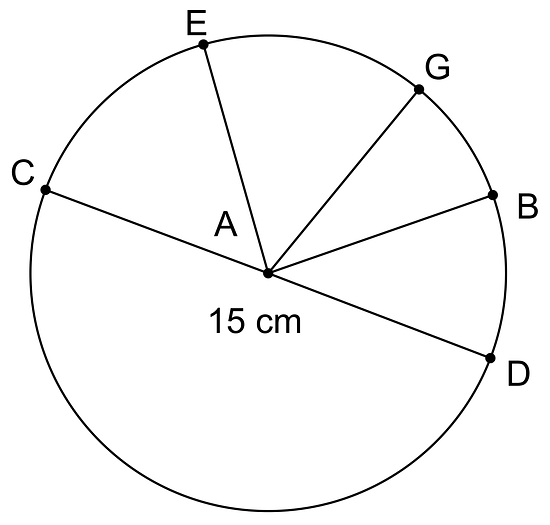
    object diameter circumference
    hula hoop 35 in
    circular pond 556 ft
    magnifying glass 5.2 cm
    car tire 71.6 in
    1. Name a segment that is a radius. How long is it?
    2. Name a segment that is a diameter. How long is it?
    Cicrle A has 5 radii of 15 centimeters
    1. Consider the equation y=1.5x +2 . Find four pairs of x and y values that make the equation true. Plot the points (x, y) on the coordinate plane.
    2. Based on the graph, can this be a proportional relationship? Why or why not?
    a blank graph