Lesson 8Reasoning about Solving Equations (Part 2)
Let’s use hangers to understand two different ways of solving equations with parentheses.
Learning Targets:
- I can explain how a balanced hanger and an equation represent the same situation.
- I can explain why some balanced hangers can be described by two different equations, one with parentheses and one without.
- I can find an unknown weight on a hanger diagram and solve an equation that represents the diagram.
- I can write an equation that describes the weights on a balanced hanger.
8.1 Equivalent to
Select all the expressions equivalent to .
8.2 Either Or
-
Explain why either of these equations could represent this hanger:
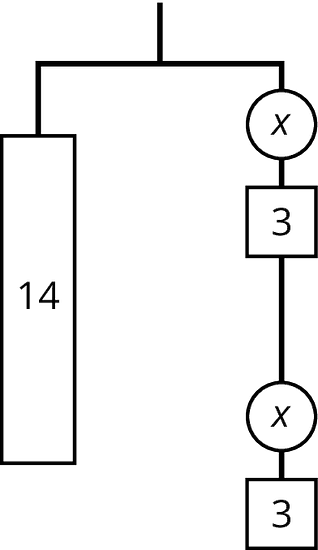
or
- Find the weight of one circle. Be prepared to explain your reasoning.
8.3 Use Hangers to Understand Equation Solving, Again
Here are some balanced hangers. Each piece is labeled with its weight.
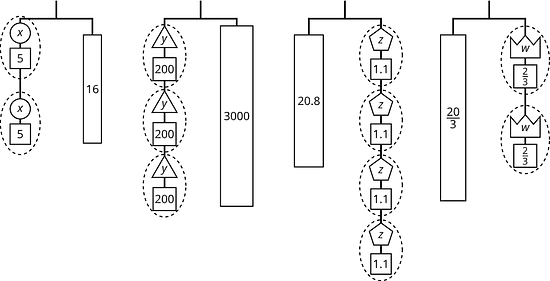
For each diagram:
- Assign one of these equations to each hanger:
- Explain how to figure out the weight of a piece labeled with a letter by reasoning about the diagram.
- Explain how to figure out the weight of a piece labeled with a letter by reasoning about the equation.
Lesson 8 Summary
The balanced hanger shows 3 equal, unknown weights and 3 2-unit weights on the left and an 18-unit weight on the right.
There are 3 unknown weights plus 6 units of weight on the left. We could represent this balanced hanger with an equation and solve the equation the same way we did before.
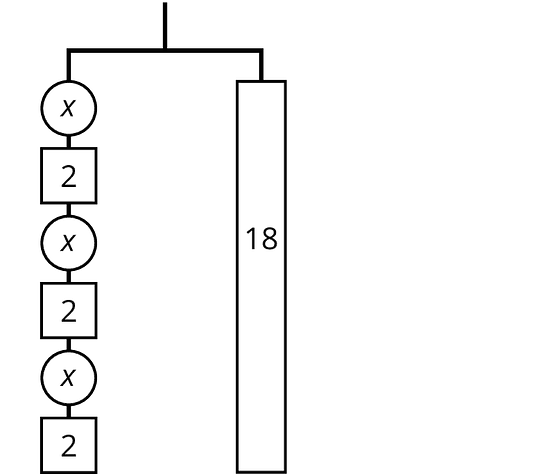
Since there are 3 groups of on the left, we could represent this hanger with a different equation: .
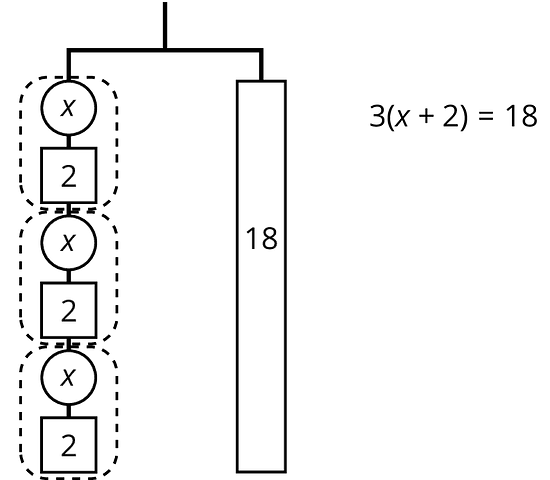
The two sides of the hanger balance with these weights: 3 groups of on one side, and 18, or 3 groups of 6, on the other side.
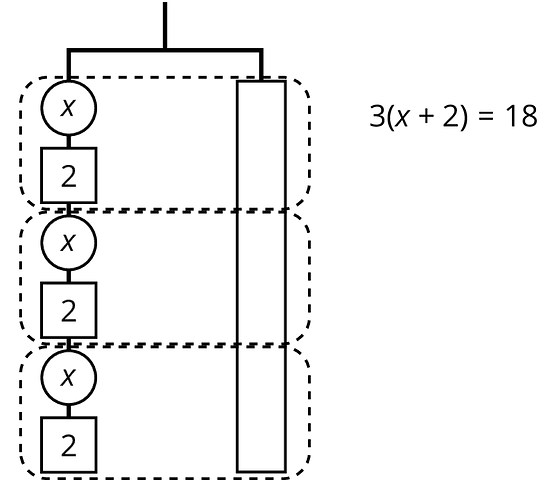
The two sides of the hanger will balance with of the weight on each side: .

We can remove 2 units of weight from each side, and the hanger will stay balanced. This is the same as subtracting 2 from each side of the equation.

An equation for the new balanced hanger is . This gives the solution to the original equation.

Here is a concise way to write the steps above:
Lesson 8 Practice Problems
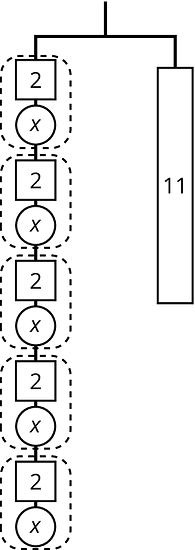
Here is a hanger:
- Write an equation to represent the hanger.
- Solve the equation by reasoning about the equation or the hanger. Explain your reasoning.
Explain how each part of the equation is represented in the hanger.
- 9
- 3
- the equal sign
Select the word from the following list that best describes each situation.
- You deposit money in a savings account, and every year the amount of money in the account increases by 2.5%.
- For every car sold, a car salesman is paid 6% of the car’s price.
- Someone who eats at a restaurant pays an extra 20% of the food price. This extra money is kept by the person who served the food.
- An antique furniture store pays $200 for a chair, adds 50% of that amount, and sells the chair for $300.
- The normal price of a mattress is $600, but it is on sale for 10% off.
- For any item you purchase in Texas, you pay an additional 6.25% of the item's price to the state government.
- Tax
- Commission
- Discount
- Markup
- Tip or gratuity
- Interest
Clare drew this diagram to match the equation , but she got the wrong solution as a result of using this diagram.
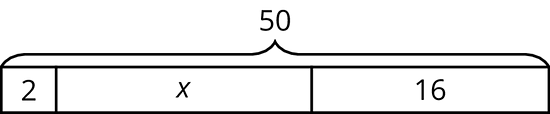
- What value for can be found using the diagram?
- Show how to fix Clare’s diagram to correctly match the equation.
- Use the new diagram to find a correct value for .
- Explain the mistake Clare made when she drew her diagram.