Lesson 9Dealing with Negative Numbers
Let’s show that doing the same to each side works for negative numbers too.
Learning Targets:
- I can use the idea of doing the same to each side to solve equations that have negative numbers or solutions.
9.1 Which One Doesn’t Belong: Rational Number Arithmetic
Which equation doesn’t belong?
9.2 Old and New Ways to Solve
Solve each equation. Be prepared to explain your reasoning.
9.3 Keeping It True
Here are some equations that all have the same solution.
- Explain how you know that each equation has the same solution as the previous equation. Pause for discussion before moving to the next question.
- Keep your work secret from your partner. Start with the equation . Do the same thing to each side at least three times to create an equation that has the same solution as the starting equation. Write the equation you ended up with on a slip of paper, and trade equations with your partner.
- See if you can figure out what steps they used to transform into their equation. When you think you know, check with them to see if you are right.
Lesson 9 Summary
When we want to find a solution to an equation, sometimes we just think about what value in place of the variable would make the equation true. Sometimes we perform the same operation on each side (for example, subtract the same amount from each side). The balanced hangers helped us to understand that doing the same to each side of an equation keeps the equation true.
Example:
Example:
Doing the same thing to each side maintains equality even if it is not helpful to solving for the unknown amount. For example, we could take the equation and add to each side:
If is true then is also true, but we are no closer to a solution than we were before adding -2. We can use moves that maintain equality to make new equations that all have the same solution. Helpful combinations of moves will eventually lead to an equation like , which gives the solution to the original equation (and every equation we wrote in the process of solving).
Lesson 9 Practice Problems
Solve each equation.
Here is an equation . Write three different equations that have the same solution as . Show or explain how you found them.
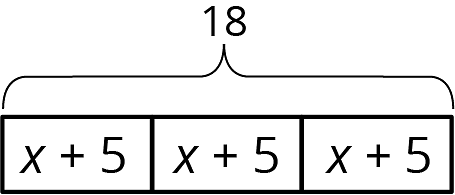
Select all the equations that match the diagram.
Match each story to an equation.
- A stack of nested paper cups is 8 inches tall. The first cup is 4 inches tall and each of the rest of the cups in the stack adds inch to the height of the stack.
- A baker uses 4 cups of flour. She uses cup to flour the counters and the rest to make 8 identical muffins.
- Elena has an 8-foot piece of ribbon. She cuts off a piece that is of a foot long and cuts the remainder into four pieces of equal length.
There are 88 seats in a theater. The seating in the theater is split into 4 identical sections. Each section has 14 red seats and some blue seats.
- Draw a tape diagram to represent the situation.
- What unknown amounts can be found by by using the diagram or reasoning about the situation?