Lesson 11Slicing Solids
Let's see what shapes you get when you slice a three-dimensional object.
Learning Targets:
- I can explain that when a three dimensional figure is sliced it creates a face that is two dimensional.
- I can picture different cross sections of prisms and pyramids.
11.1 Prisms, Pyramids, and Polyhedra
Describe each shape as precisely as you can. Click on the applet and drag the mouse to show the object turning in 3D.
11.2 What's the Cross Section?
Here are a rectangular prism and a pyramid with the same base and same height. Drag the large red point up and down to move the plane through the solids.
-
If we slice each solid parallel to its base halfway up, what shape cross sections would we get? What is the same about the cross sections? What is different?
-
If we slice each solid parallel to its base near the top, what shape cross sections would we get? What is the same about the cross sections? What is different?
Are you ready for more?
Describe the cross sections that would result from slicing each solid perpendicular to its base.
11.3 Card Sort: Cross Sections
11.4 Drawing Cross Sections
Use the applet to draw each cross section and describe it in words.
-
Here is an applet with a rectangular prism, 4 units by 2 units by 3 units.
- A plane cuts the prism parallel to the bottom and top faces.
- The plane moves up and cuts the prism at a different height.
- A vertical plane cuts the prism diagonally.
- A square pyramid has a base that is 4 units by 4 units. Its height is also 4 units.
- A plane cuts the pyramid parallel to the base.
- A vertical plane cuts the prism.
- A cube has an edge of length 4.
- A plane cuts off the corner of the cube.
- The plane moves farther from the corner and makes a cut through the middle of the cube.
Lesson 11 Summary
When we slice a three-dimensional object, we expose new faces that are two dimensional. The two-dimensional face is a cross section. Many different cross sections are possible when slicing the same three-dimensional object.
Here are two peppers. One is sliced horizontally, and the other is sliced vertically, producing different cross sections.

The imprints of the slices represent the two-dimensional faces created by each slice.
It takes practice imagining what the cross section of a three-dimensional object will be for different slices. It helps to experiment and see for yourself what happens!
Glossary Terms
A cross section is the new face you see when you slice through a three-dimensional figure.
For example, if you slice a rectangular pyramid parallel to the base, you get a smaller rectangle as the cross section.
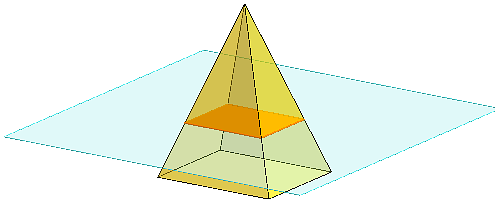
Lesson 11 Practice Problems
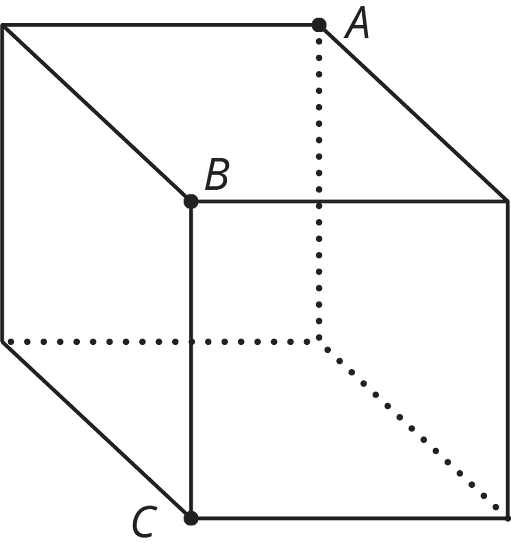
A cube is cut into two pieces by a single slice that passes through points , , and . What shape is the cross section?
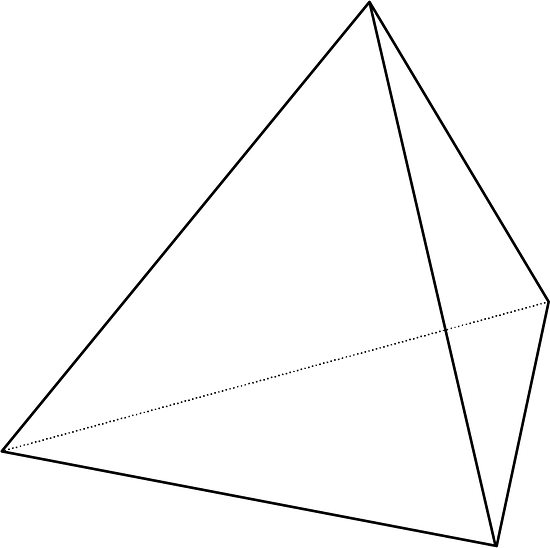
Describe how to slice the three-dimensional figure to result in each cross section.
Three-dimensional figure:
Cross sections:

Here are two three-dimensional figures.
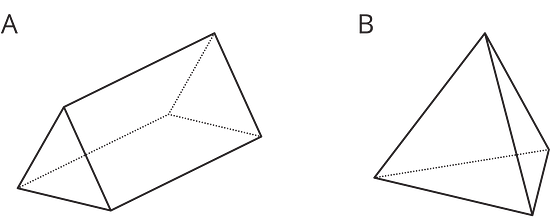 Describe a way to slice one of the figures so that the cross section is a rectangle.
Describe a way to slice one of the figures so that the cross section is a rectangle.Each row contains the degree measures of two supplementary angles. Complete the table.
measure of
an anglemeasure of
its supplementTwo months ago, the price, in dollars, of a cell phone was .
- Last month, the price of the phone increased by 10%. Write an expression for the price of the phone last month.
- This month, the price of the phone decreased by 10%. Write an expression for the price of the phone this month.
- Is the price of the phone this month the same as it was two months ago? Explain your reasoning.