Lesson 10Drawing Triangles (Part 2)
Let’s draw some more triangles.
Learning Targets:
- Given two side lengths and one angle measure, I can draw different triangles with these measurements or show that these measurements determine one unique triangle or no triangle.
10.1 Using a Compass to Estimate Length
- Draw a angle.
- Use a compass to make sure both sides of your angle have a length of 5 centimeters.
- If you connect the ends of the sides you drew to make a triangle, is the third side longer or shorter than 5 centimeters? How can you use a compass to explain your answer?
10.2 Revisiting How Many Can You Draw?
Use the applet to draw triangles.
-
Draw as many different triangles as you can with each of these sets of measurements:
- One angle measures , one side measures 4 cm and one side measures 5 cm.
- Two sides measure 6 cm and one angle measures .
-
Did either of these sets of measurements determine one unique triangle? How do you know?
10.3 Three Angles
Use the applet to draw triangles. Sides can overlap.
- Draw as many different triangles as you can with each of these sets of measurements:
- One angle measures , one measures , and one measures .
- One angle measures , one measures , and one measures .
- Did either of these sets of measurements determine one unique triangle? How do you know?
Are you ready for more?
Using only the point, segment, and compass tools provided, create an equilateral triangle. You are only successful if the triangle remains equilateral while dragging its vertices around.
Lesson 10 Summary
A triangle has six measures: three side lengths and three angle measures.
If we are given three measures, then sometimes, there is no triangle that can be made. For example, there is no triangle with side lengths 1, 2, 5, and there is no triangle with all three angles measuring .
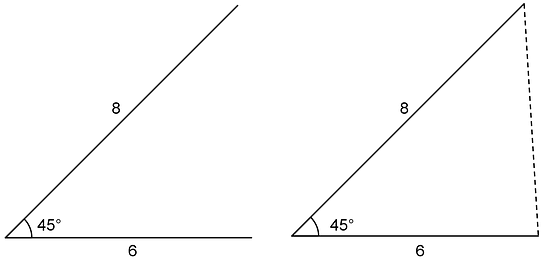
Sometimes, only one triangle can be made. By this we mean that any triangle we make will be the same, having the same six measures. For example, if a triangle can be made with three given side lengths, then the corresponding angles will have the same measures. Another example is shown here: an angle measuring between two side lengths of 6 and 8 units. With this information, one unique triangle can be made.
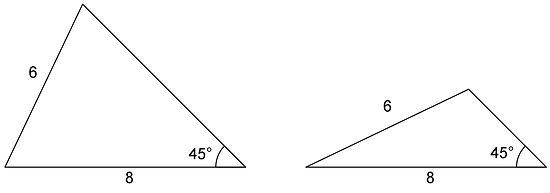
Sometimes, two or more different triangles can be made with three given measures. For example, here are two different triangles that can be made with an angle measuring and side lengths 6 and 8. Notice the angle is not between the given sides.
Three pieces of information about a triangle’s side lengths and angle measures may determine no triangles, one unique triangle, or more than one triangle. It depends on the information.
Lesson 10 Practice Problems
A triangle has sides of length 7 cm, 4 cm, and 5 cm. How many unique triangles can be drawn that fit that description? Explain or show your reasoning.
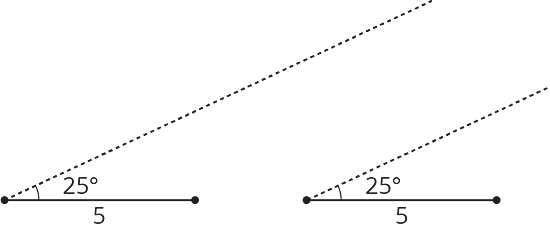
A triangle has one side that is 5 units long and an adjacent angle that measures . The two other angles in the triangle measure and . Complete the two diagrams to create two different triangles with these measurements.
Is it possible to make a triangle that has angles measuring 90 degrees, 30 degrees, and 100 degrees? If so, draw an example. If not, explain your reasoning.
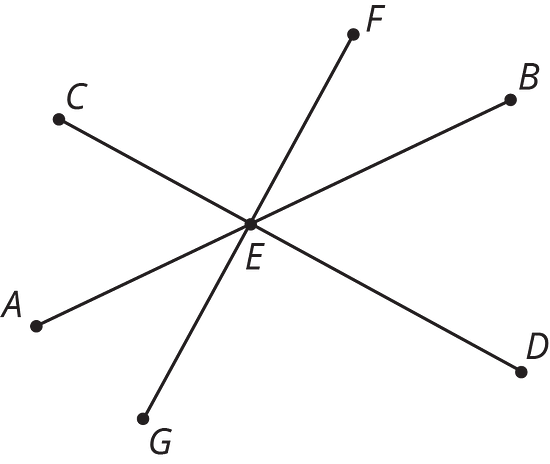
Segments , , and intersect at point . Angle is a right angle. Identify any pairs of angles that are complementary.
Match each equation to a step that will help solve the equation for .
- Add to each side.
- Add to each side.
- Add to each side.
- Add to each side.
- Multiply each side by 3.
- Multiply each side by .
- Multiply each side by .
- Multiply each side by .
- If you deposit $300 in an account with a 6% interest rate, how much will be in your account after 1 year?
- If you leave this money in the account, how much will be in your account after 2 years?