Lesson 9Drawing Triangles (Part 1)
Let’s see how many different triangles we can draw with certain measurements.
Learning Targets:
- Given two angle measures and one side length, I can draw different triangles with these measurements or show that these measurements determine one unique triangle or no triangle.
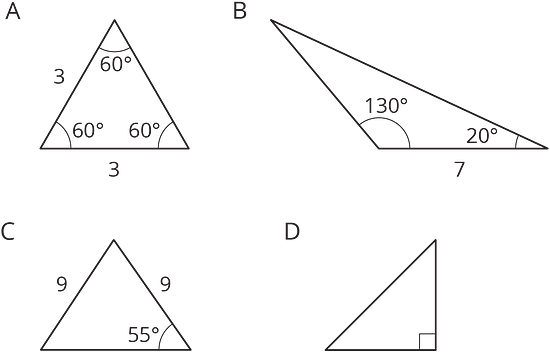
9.1 Which One Doesn’t Belong: Triangles
Which one doesn’t belong?
9.2 Does Your Triangle Match Theirs?
Three students have each drawn a triangle. For each description of a student’s triangle:
-
Drag the vertices to create a triangle with the given measurements.
- Compare their measurements to the other side lengths and angle measures in your triangle.
-
Decide whether the triangle you made must be an identical copy of the triangle that the student drew. Explain your reasoning.
Jada’s triangle has one angle measuring 75°.
Andre’s triangle has one angle measuring 75° and one angle measuring 45°.
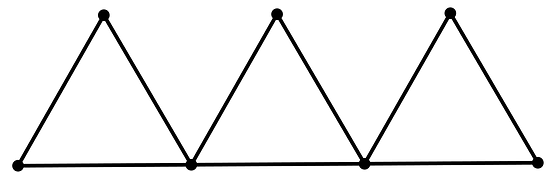
9.3 How Many Can You Draw?
-
Draw as many different triangles as you can with each of these sets of measurements:
- Two angles measure , and one side measures 4 cm.
- Two angles measure , and one side measures 4 cm.
- One angle measures , one angle measures , and one side measures 4 cm.
-
Which sets of measurements determine one unique triangle? Explain or show your reasoning.
Are you ready for more?
Lesson 9 Summary
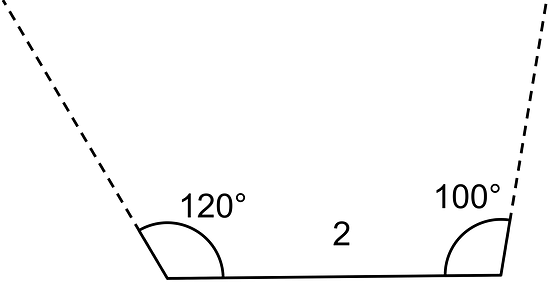
Sometimes, we are given two different angle measures and a side length, and it is impossible to draw a triangle. For example, there is no triangle with side length 2 and angle measures and :
Sometimes, we are given two different angle measures and a side length between them, and we can draw a unique triangle. For example, if we draw a triangle with a side length of 4 between angles and , there is only one way they can meet up and complete to a triangle:
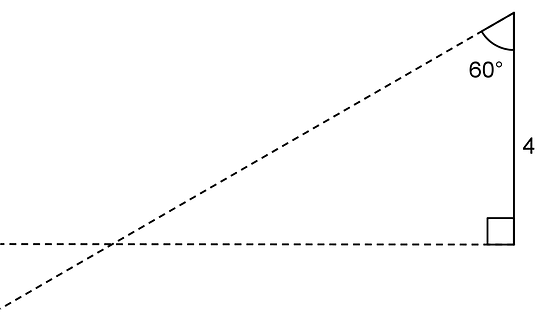
Any triangle drawn with these three conditions will be identical to the one above, with the same side lengths and same angle measures.
Lesson 9 Practice Problems
Use a protractor to try to draw each triangle. Which of these three triangles is impossible to draw?
- A triangle where one angle measures and another angle measures
- A triangle where one angle measures and another angle measures
-
A triangle where one angle measures and another angle measures
A triangle has an angle measuring , an angle measuring , and a side that is 6 units long. The 6-unit side is in between the and angles.
- Sketch this triangle and label your sketch with the given measures.
- How many unique triangles can you draw like this?
- Find a value for that makes less than .
- Find a value for that makes greater than .
One of the particles in atoms is called an electron. It has a charge of -1. Another particle in atoms is a proton. It has charge of +1.
The overall charge of an atom is the sum of the charges of the electrons and the protons. Here is a list of common elements.
charge from
electronscharge from
protonsoverall
chargecarbon -6 +6 0 aluminum -10 +13 phosphide -18 +15 iodide -54 +53 tin -50 +50 Find the overall charge for the rest of the atoms on the list.
A factory produces 3 bottles of sparkling water for every 7 bottles of plain water. If those are the only two products they produce, what percentage of their production is sparkling water? What percentage is plain?