Lesson 8Triangles with 3 Common Measures
Let’s contrast triangles.
Learning Targets:
- I understand that changing which sides and angles are next to each other can make different triangles.
8.1 3 Sides; 3 Angles
Examine each set of triangles. What do you notice? What is the same about the triangles in the set? What is different?
Set 1:
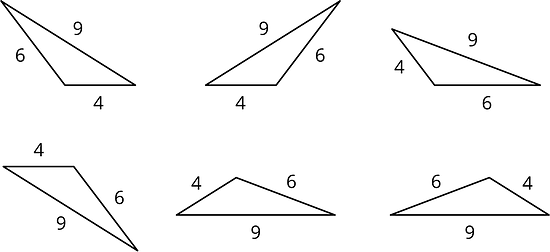
Set 2:
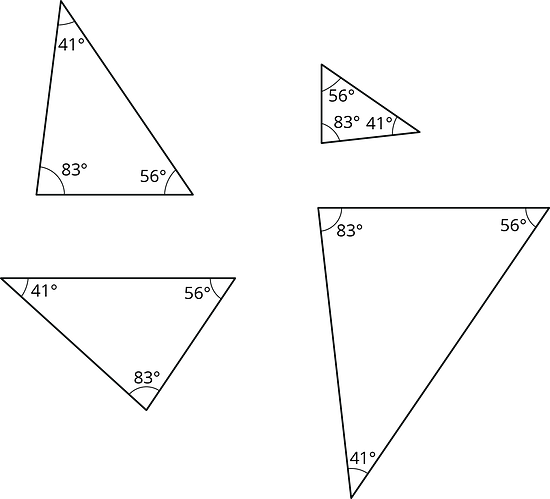
8.2 2 Sides and 1 Angle
Examine this set of triangles.

- What is the same about the triangles in the set? What is different?
-
How many different triangles are there? Explain or show your reasoning.
8.3 2 Angles and 1 Side
Examine this set of triangles.
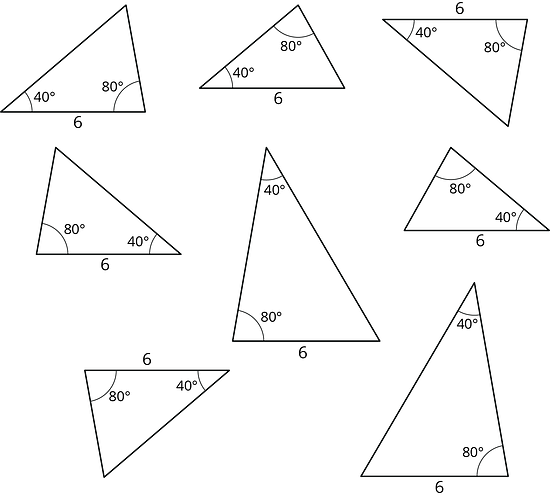
- What is the same about the triangles in the set? What is different?
-
How many different triangles are there? Explain or show your reasoning.
Are you ready for more?
Lesson 8 Summary
Both of these quadrilaterals have a right angle and side lengths 4 and 5:
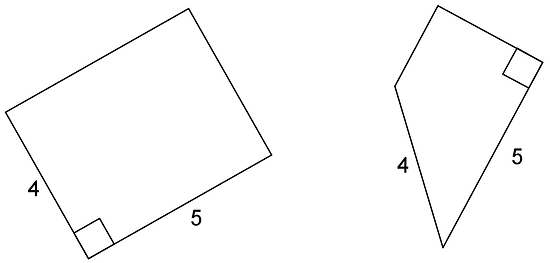
However, in one case, the right angle is between the two given side lengths; in the other, it is not.
If we create two triangles with three equal measures, but these measures are not next to each other in the same order, that usually means the triangles are different. Here is an example:
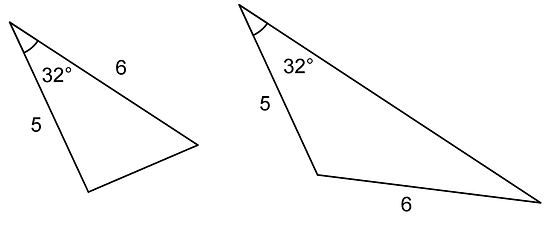
Lesson 8 Practice Problems
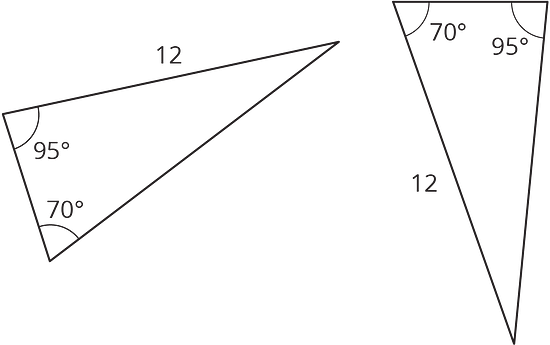
Are these two triangles identical? Explain how you know.
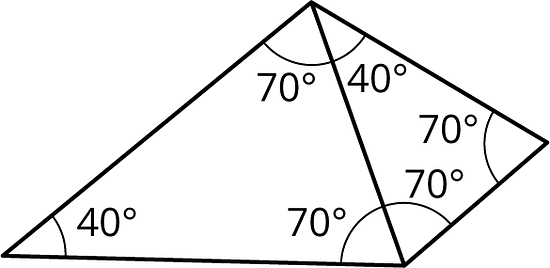
Are these triangles identical? Explain your reasoning.
- Tyler claims that if two triangles each have a side length of 11 units and a side length of 8 units, and also an angle measuring , they must be identical to each other. Do you agree? Explain your reasoning.
The markings on the number line are equally spaced. Label the other markings on the number line.

A passenger on a ship dropped his camera into the ocean. If it is descending at a rate of -4.2 meters per second, how long until it hits the bottom of the ocean, which is at -1,875 meters?
Apples cost $1.99 per pound.
- How much do pounds of apples cost?
- How much do pounds of apples cost?
- Clare spent $5.17 on apples. How many pounds of apples did Clare buy?
Diego has a glue stick with a diameter of 0.7 inches. He sets it down 3.5 inches away from the edge of the table, but it rolls onto the floor. How many rotations did the glue stick make before it fell off of the table?