Lesson 7Building Polygons (Part 2)
Let’s build more triangles.
Learning Targets:
- I can reason about a figure with an unknown angle.
- I can show whether or not 3 side lengths will make a triangle.
7.1 Where Is Lin?
At a park, the slide is 5 meters east of the swings. Lin is standing 3 meters away from the slide.
-
Draw a diagram of the situation including a place where Lin could be.
-
How far away from the swings is Lin in your diagram?
-
Where are some other places Lin could be?
7.2 How Long Is the Third Side?
Use the applet to answer the questions.
-
Build as many different triangles as you can that have one side length of 5 inches and one of 4 inches. Record the side lengths of each triangle you build.
-
Are there lengths that could be used for the third side of the triangle that aren't values of the sliders?
-
Are there lengths that are values of the sliders that could not be used as the third side of the triangle?
Are you ready for more?
Assuming you had access to strips of any length, and you used the 9-inch and 5-inch strips as the first two sides, complete the sentences:
- The third side can't be _____ inches or longer.
- The third side can't be _____ inches or shorter.
7.3 Swinging the Sides Around
Use the applet to answer the questions.
-
If you wanted to make a triangle with side lengths of 3 units, 3 units, and 4 units, how would you know at what angle you should position the sides?
-
Let segment be the 3-unit side length. Right-click on point , check Trace On, and drag point .

-
What path does point trace as you move it around? Why? What other tool do we have in our geometry toolkit that could do something similar?
-
Using 2 different colors, draw 2 different triangles that would have the 4-unit segment as their base and a 3-unit segment for their right side.
-
Right-click on point , uncheck Trace On.
-
Repeat the previous instructions, letting segment be the 3-unit side length.
-
Using a third color, draw a point where the two traces intersect. Next, draw another triangle that would have segment as its base and segments and for both of its other sides.
-
If you had used segments that were only 2 units long on either end of segment , how would that have affected your drawing?
Lesson 7 Summary
If we want to build a polygon with two given side lengths that share a vertex, we can think of them as being connected by a hinge that can be opened or closed:


You may have noticed that sometimes it is not possible to build a polygon given a set of lengths. For example, if we have one really, really long segment and a bunch of short segments, we may not be able to connect them all up. Here's what happens if you try to make a triangle with side lengths 21, 4, and 2:


If we draw circles of radius 4 and 2 on the endpoints of the side of length 21 to represent positions for the shorter sides, we can see that there are no places for the short sides that would allow them to meet up and form a triangle.
In general, the longest side length must be less than the sum of the other two side lengths. If not, we can’t make a triangle!
If we can make a triangle with three given side lengths, it turns out that the measures of the corresponding angles will always be the same. For example, if two triangles have side lengths 3, 4, and 5, they will have the same corresponding angle measures.
Lesson 7 Practice Problems
In the diagram, the length of segment is 10 units and the radius of the circle centered at is 4 units. Use this to create two unique triangles, each with a side of length 10 and a side of length 4. Label the sides that have length 10 and 4.
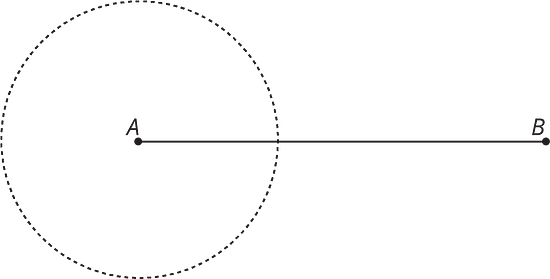
Select all the sets of three side lengths that will make a triangle.
- 3, 4, 8
- 7, 6, 12
- 5, 11, 13
- 4, 6, 12
- 4, 6, 10
- Based on signal strength, a person knows their lost phone is exactly 47 feet from the nearest cell tower. The person is currently standing 23 feet from the same cell tower. What is the closest the phone could be to the person? What is the furthest their phone could be from them?
Each row contains the degree measures of two complementary angles. Complete the table.
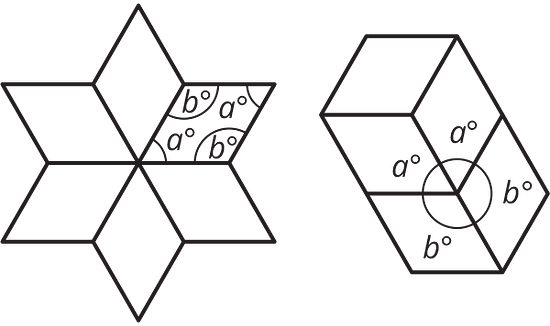
measure of an angle measure of its complement Here are two patterns made using identical rhombuses. Without using a protractor, determine the value of and . Explain or show your reasoning.
Mai’s family is traveling in a car at a constant speed of 65 miles per hour.
- At that speed, how long will it take them to travel 200 miles?
- How far do they travel in 25 minutes?