Lesson 6Building Polygons (Part 1)
Let’s build shapes.
Learning Targets:
- I can show that the 3 side lengths that form a triangle cannot be rearranged to form a different triangle.
- I can show that the 4 side lengths that form a quadrilateral can be rearranged to form different quadrilaterals.
6.1 True or False: Signed Numbers
Decide whether each equation is true or false. Be prepared to explain your reasoning.
6.2 What Can You Build?
- Use the segments in the applet to build several polygons, including at least one triangle and one quadrilateral.
- After you finish building several polygons, select one triangle and one quadrilateral that you have made.
- Measure all the angles in the two shapes you selected. Note: select points in order counterclockwise, like a protractor.
- Using these measurements along with the side lengths as marked, draw your triangle and quadrilateral as accurately as possible on separate paper.
6.3 Building Diego’s and Jada’s Shapes
- Diego built a quadrilateral using side lengths of 4 in, 5 in, 6 in, and 9 in.
- Build such a shape.
- Is your shape an identical copy of Diego’s shape? Explain your reasoning.
- Jada built a triangle using side lengths of 4 in, 5 in, and 8 in.
- Build such a shape.
- Is your shape an identical copy of Jada’s shape? Explain your reasoning.
6.4 Building Han’s Shape
Han built a shape using side lengths of 3 in, 4 in, and 9 in.
- Build such a shape.
- What do you notice?
Lesson 6 Summary
Sometimes we are given a polygon and asked to find the lengths of the sides. What options do you have if you need to build a polygon with some side lengths? Sometimes, we can make lots of different figures. For example, if you have side lengths 5, 7, 11, and 14, here are some of the many, many quadrilaterals we can make with those side lengths:
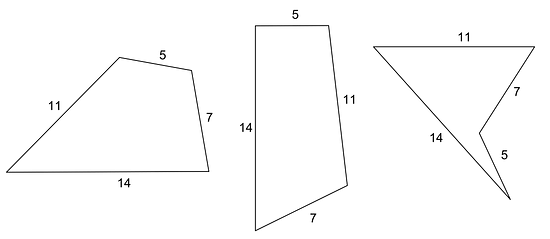
Sometimes, it is not possible to make a figure with certain side lengths. For example, 18, 1, 1, 1 (try it!).
We will continue to investigate the figures that can be made with given measures.
Lesson 6 Practice Problems
A rectangle has side lengths of 6 units and 3 units. Could you make a quadrilateral that is not identical using the same four side lengths? If so, describe it.
Come up with an example of three side lengths that can not possibly make a triangle, and explain how you know.
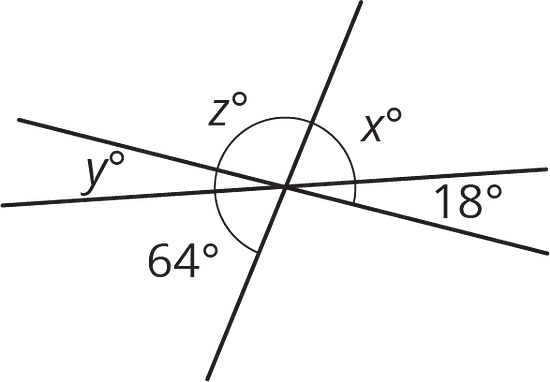
Find , , and .
How many right angles need to be put together to make:
- 360 degrees?
- 180 degrees?
- 270 degrees?
- A straight angle?
Solve each equation.
- You can buy 4 bottles of water from a vending machine for $7. At this rate, how many bottles of water can you buy for $28? If you get stuck, consider creating a table.
- It costs $20 to buy 5 sandwiches from a vending machine. At this rate, what is the cost for 8 sandwiches? If you get stuck, consider creating a table.