Lesson 5Using Equations to Solve for Unknown Angles
Let’s figure out missing angles using equations.
Learning Targets:
- I can write an equation to represent a relationship between angle measures and solve the equation to find unknown angle measures.
5.1 Is This Enough?
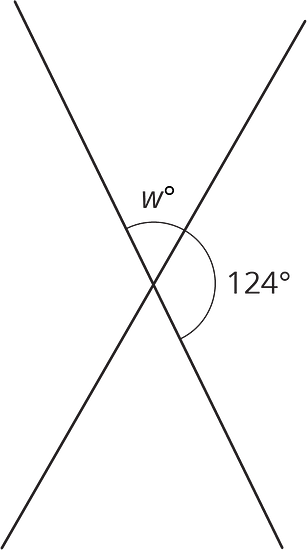
Tyler thinks that this figure has enough information to figure out the values of and .

Do you agree? Explain your reasoning.
5.2 What Does It Look Like?
Elena and Diego each wrote equations to represent these diagrams. For each diagram, decide which equation you agree with, and solve it. You can assume that angles that look like right angles are indeed right angles.
- Elena:
Diego:

- Elena:
Diego:

- Elena:
Diego:

- Elena:
Diego:

- Elena:
Diego:

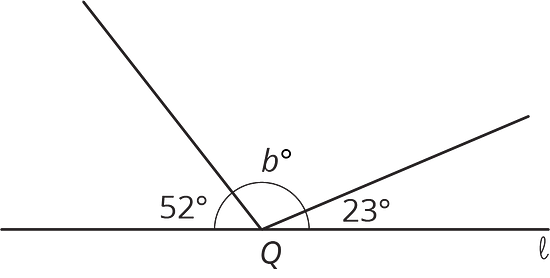
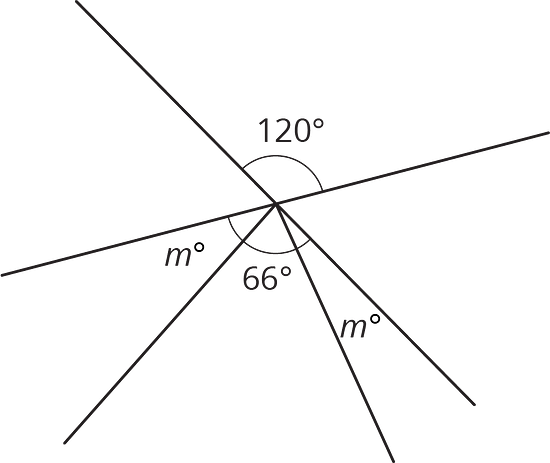
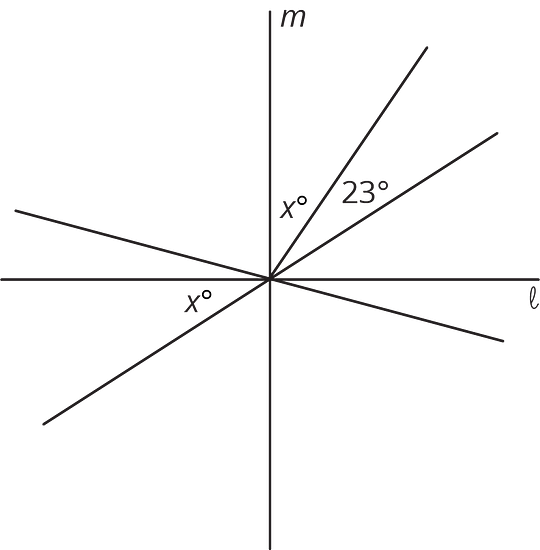
5.3 Calculate the Measure
Find the unknown angle measures. Show your thinking. Organize it so it can be followed by others.
- Lines and are perpendicular.
Are you ready for more?
The diagram contains three squares. Three additional segments have been drawn that connect corners of the squares. We want to find the exact value of .
- Use a protractor to measure the three angles. Use your measurements to conjecture about the value of .
- Find the exact value of by reasoning about the diagram.

Lesson 5 Summary
To find an unknown angle measure, sometimes it is helpful to write and solve an equation that represents the situation. For example, suppose we want to know the value of in this diagram.

Using what we know about vertical angles, we can write the equation to represent this situation. Then we can solve the equation.
Lesson 5 Practice Problems
Segments , , and intersect at point . Angle measures . Find the value of .
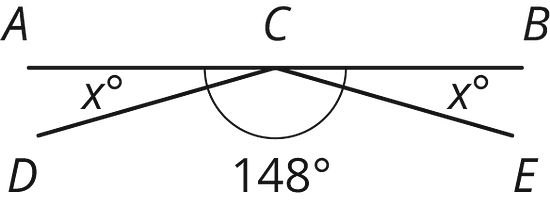
Line is perpendicular to line . Find the value of and .
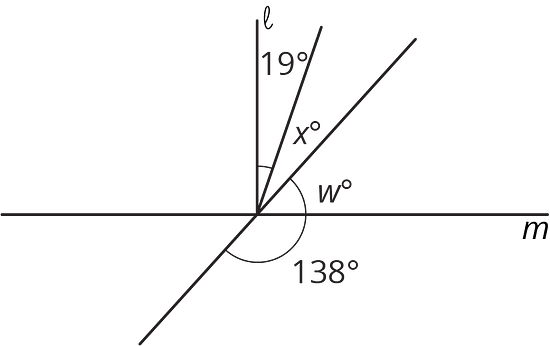
If you knew that two angles were complementary and were given the measure of one of those angles, would you be able to find the measure of the other angle? Explain your reasoning.
For each inequality, decide whether the solution is represented by or .
A runner ran of a 5 kilometer race in 21 minutes. They ran the entire race at a constant speed.
- How long did it take to run the entire race?
- How many minutes did it take to run 1 kilometer?
Jada, Elena, and Lin walked a total of 37 miles last week. Jada walked 4 more miles than Elena, and Lin walked 2 more miles than Jada. The diagram represents this situation:
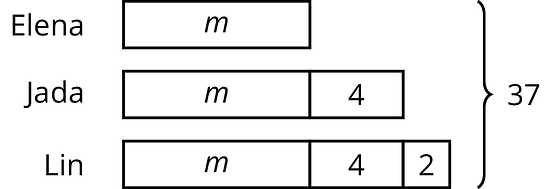
Find the number of miles that they each walked. Explain or show your reasoning.
Select all the expressions that are equivalent to .