Lesson 4Solving for Unknown Angles
Let’s figure out some missing angles.
Learning Targets:
- I can reason through multiple steps to find unknown angle measures.
- I can recognize when an equation represents a relationship between angle measures.
4.1 True or False: Length Relationships
Here are some line segments.

Decide if each of these equations is true or false. Be prepared to explain your reasoning.
4.2 Info Gap: Angle Finding
Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.
If your teacher gives you the problem card:
- Silently read your card and think about what information you need to answer the question.
- Ask your partner for the specific information that you need.
- Explain to your partner how you are using the information to solve the problem.
- Solve the problem and explain your reasoning to your partner.
If your teacher gives you the data card:
- Silently read the information on your card.
- Ask your partner “What specific information do you need?” and wait for your partner to ask for information. Only give information that is on your card. (Do not figure out anything for your partner!)
- Before telling your partner the information, ask “Why do you need that information?”
- After your partner solves the problem, ask them to explain their reasoning and listen to their explanation.
4.3 What’s the Match?
Match each figure to an equation that represents what is seen in the figure. For each match, explain how you know they are a match.

Are you ready for more?
- What is the angle between the hour and minute hands of a clock at 3:00?
- You might think that the angle between the hour and minute hands at 2:20 is 60 degrees, but it is not! The hour hand has moved beyond the 2. Calculate the angle between the clock hands at 2:20.
- Find a time where the hour and minute hand are 40 degrees apart. (Assume that the time has a whole number of minutes.) Is there just one answer?
Lesson 4 Summary
We can write equations that represent relationships between angles.

- The first pair of angles are supplementary, so .
- The second pair of angles are vertical angles, so .
- The third pair of angles are complementary, so .
Lesson 4 Practice Problems
is a point on line segment . is a line segment. Select all the equations that represent the relationship between the measures of the angles in the figure.
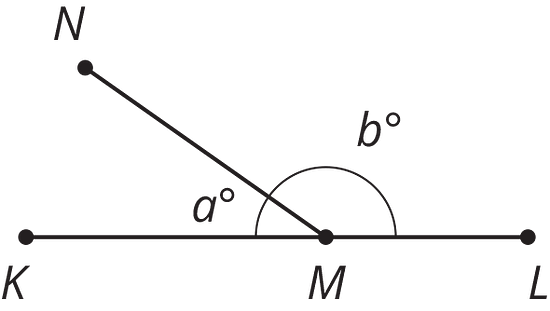
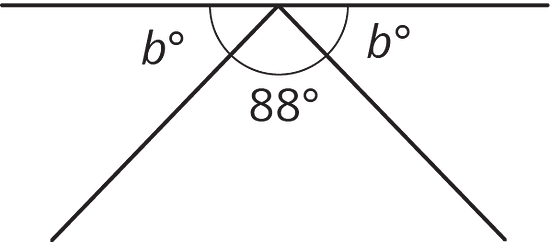
Which equation represents the relationship between the angles in the figure?
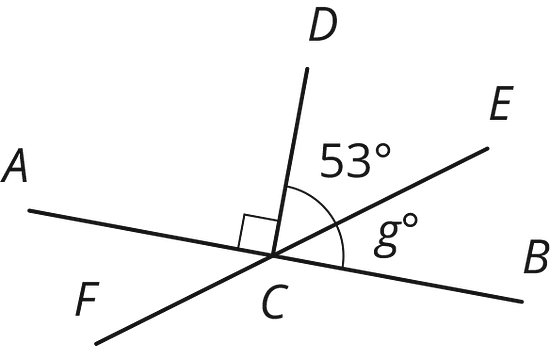
Segments , , and intersect at point , and angle is a right angle. Find the value of .
Select all the expressions that are the result of decreasing by 80%.
Andre is solving the equation . He says, “I can subtract from each side to get and then divide by 4 to get .” Kiran says, “I think you made a mistake.”
- How can Kiran know for sure that Andre’s solution is incorrect?
- Describe Andre’s error and explain how to correct his work.
Solve each equation.
A train travels at a constant speed for a long distance. Write the two constants of proportionality for the relationship between distance traveled and elapsed time. Explain what each of them means.
time elapsed (hr) distance (mi) 1.2 54 3 135 4 180