Lesson 13Decomposing Bases for Area
Let’s look at how some people use volume.
Learning Targets:
- I can calculate the volume of a prism with a complicated base by decomposing the base into quadrilaterals or triangles.
13.1 Are These Prisms?
-
Which of these solids are prisms? Explain how you know.
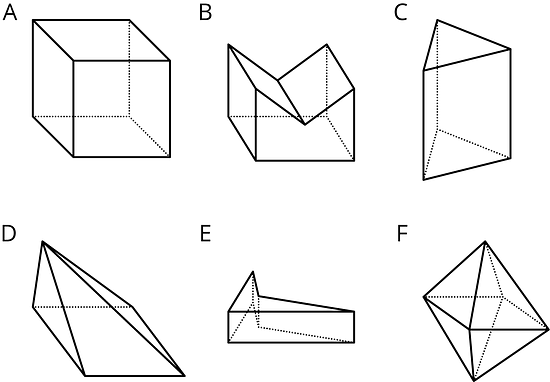
-
For each of the prisms, what does the base look like?
- Shade one base in the picture.
-
Draw a cross section of the prism parallel to the base.
13.2 A Box of Chocolates
A box of chocolates is a prism with a base in the shape of a heart and a height of 2 inches. Here are the measurements of the base.
To calculate the volume of the box, three different students have each drawn line segments showing how they plan on finding the area of the heart-shaped base.
- For each student’s plan, describe the shapes the student must find the area of and the operations they must use to calculate the total area.
- Although all three methods could work, one of them requires measurements that are not provided. Which one is it?
- Between you and your partner, decide which of you will use which of the remaining two methods.
- Using the quadrilaterals and triangles drawn in your selected plan, find the area of the base.
- Trade with a partner and check each other’s work. If you disagree, work to reach an agreement.
-
Return their work. Calculate the volume of the box of chocolates.
Are you ready for more?
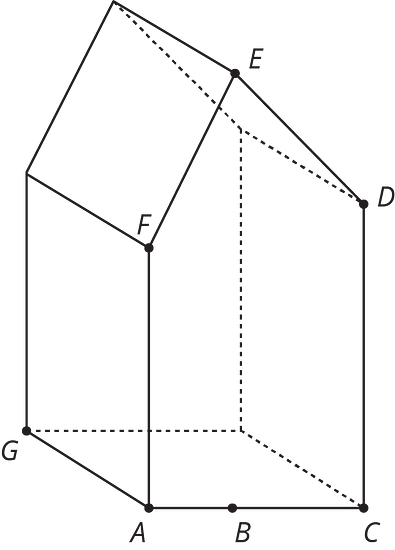
13.3 Another Prism
A house-shaped prism is created by attaching a triangular prism on top of a rectangular prism.

-
Draw the base of this prism and label its dimensions.
- What is the area of the base? Explain or show your reasoning.
- What is the volume of the prism?
Lesson 13 Summary
To find the area of any polygon, you can decompose it into rectangles and triangles. There are always many ways to decompose a polygon.

Sometimes it is easier to enclose a polygon in a rectangle and subtract the area of the extra pieces.
To find the volume of a prism with a polygon for a base, you find the area of the base, , and multiply by the height, .
Lesson 13 Practice Problems
You find a crystal in the shape of a prism. Find the volume of the crystal.
The point is directly underneath point , and the following lengths are known:
- From to : 2 mm
- From to : 3 mm
- From to : 6 mm
- From to : 10 mm
- From to : 7 mm
- From to : 4 mm
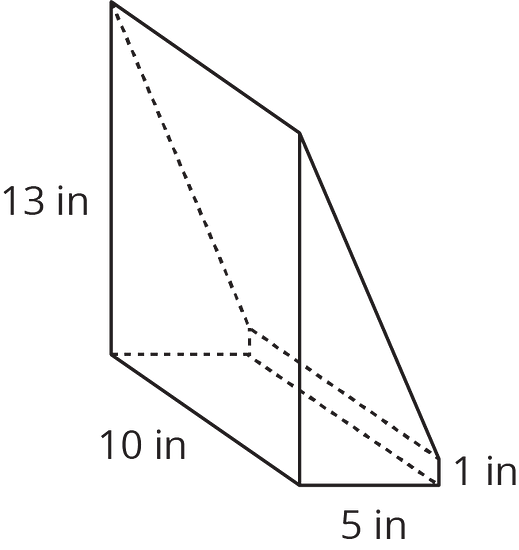
A rectangular prism with dimensions 5 inches by 13 inches by 10 inches was cut to leave a piece as shown in the image. What is the volume of this piece? What is the volume of the other piece not pictured?
A triangle has one side that is 7 cm long and another side that is 3 cm long.
- Sketch this triangle and label your sketch with the given measures. (If you are stuck, try using a compass or cutting some straws to these two lengths.)
- Draw one more triangle with these measures that is not identical to your first triangle.
- Explain how you can tell they are not identical.
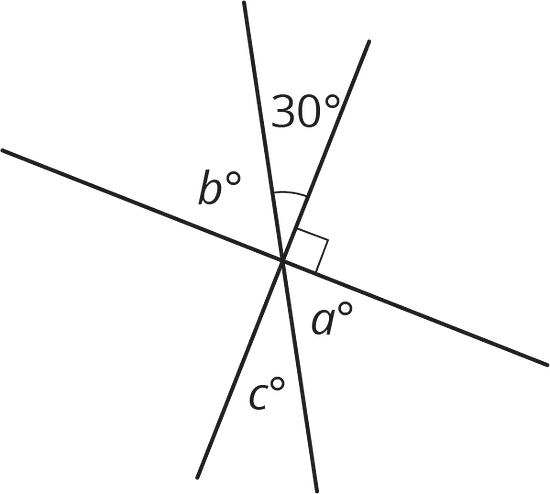
Select all equations that represent a relationship between angles in the figure.
A mixture of punch contains 1 quart of lemonade, 2 cups of grape juice, 4 tablespoons of honey, and gallon of sparkling water. Find the percentage of the punch mixture that comes from each ingredient. Round your answers to the nearest tenth of a percent. (Hint: 1 cup = 16 tablespoons)