Lesson 14Surface Area of Right Prisms
Let’s look at the surface area of prisms.
Learning Targets:
- I can find and use shortcuts when calculating the surface area of a prism.
- I can picture the net of a prism to help me calculate its surface area.
14.1 Multifaceted
Your teacher will show you a prism.
- What are some things you could measure about the object?
-
What units would you use for these measurements?
14.2 So Many Faces
Here is a picture of your teacher's prism:

Three students are trying to calculate the surface area of this prism.
- Noah says, “This is going to be a lot of work. We have to find the areas of 14 different faces and add them up.”
- Elena says, “It’s not so bad. All 12 rectangles are identical copies, so we can find the area for one of them, multiply that by 12 and then add on the areas of the 2 bases.”
- Andre says, “Wait, I see another way! Imagine unfolding the prism into a net. We can use 1 large rectangle instead of 12 smaller ones.”
- Do you agree with any of them? Explain your reasoning.
- How big is the “1 large rectangle” Andre is talking about? Explain or show your reasoning. If you get stuck, consider drawing a net for the prism.
- Will Noah’s method always work for finding the surface area of any prism? Elena’s method? Andre’s method? Be prepared to explain your reasoning.
-
Which method do you prefer? Why?
14.3 Revisiting a Pentagonal Prism
-
Between you and your partner, choose who will use each of these two methods to find the surface area of the prism.
- Adding the areas of all the faces
- Using the perimeter of the base.
- Use your chosen method to calculate the surface area of the prism. Show your thinking. Organize it so it can be followed by others.
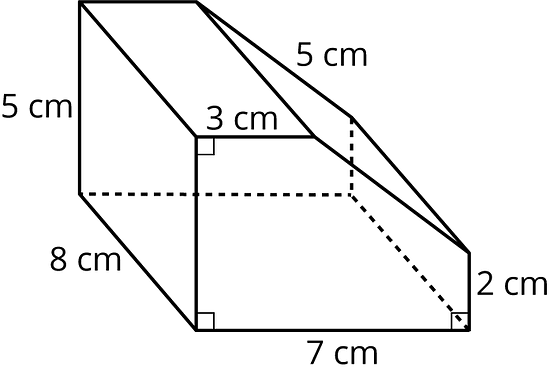
- Trade papers with your partner, and check their work. Discuss your thinking. If you disagree, work to reach an agreement.
Are you ready for more?


In a deck of cards, each card measures 6 cm by 9 cm.
-
When stacked, the deck is 2 cm tall, as shown in the first photo. Find the volume of this deck of cards.
-
Then the cards are fanned out, as shown in the second picture. The distance from the rightmost point on the bottom card to the rightmost point on the top card is now 7 cm instead of 2 cm. Find the volume of the new stack.
Lesson 14 Summary
To find the surface area of a three-dimensional figure whose faces are made up of polygons, we can find the area of each face, and add them up!
Sometimes there are ways to simplify our work. For example, all of the faces of a cube with side length are the same. We can find the area of one face, and multiply by 6. Since the area of one face of a cube is , the surface area of a cube is .
We can use this technique to make it faster to find the surface area of any figure that has faces that are the same.
For prisms, there is another way. We can treat the prism as having three parts: two identical bases, and one long rectangle that has been taped along the edges of the bases. The rectangle has the same height as the prism, and its width is the perimeter of the base. To find the surface area, add the area of this rectangle to the areas of the two bases.
Lesson 14 Practice Problems
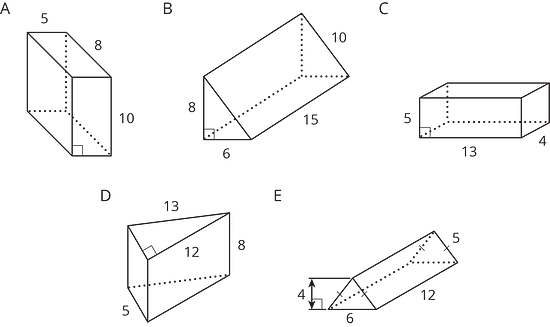
Edge lengths are given in units. Find the surface area of each prism in square units.
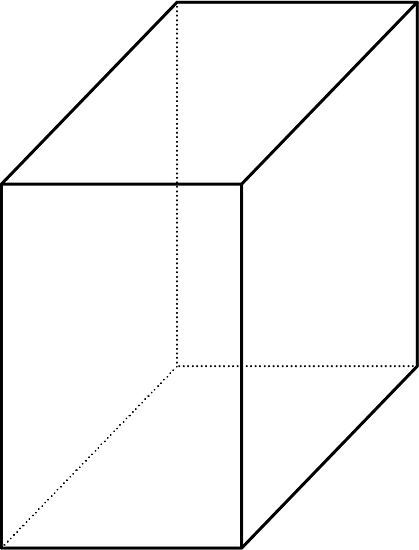
Priya says, “No matter which way you slice this rectangular prism, the cross section will be a rectangle.” Mai says, “I’m not so sure.” Describe a slice that Mai might be thinking of.
is the intersection of line and line . Find the measure of each of the angles.
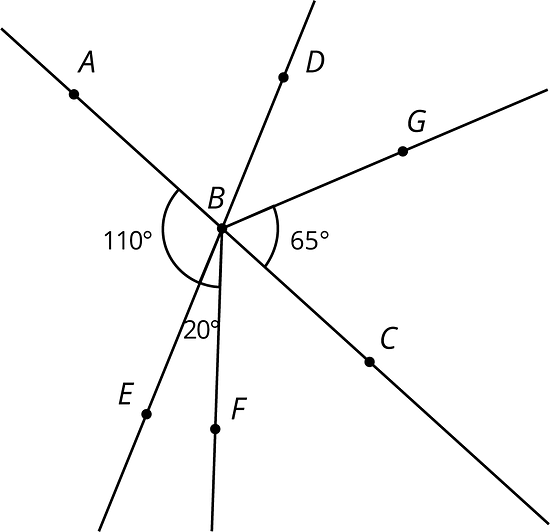
-
The measure of angle
-
The measure of angle
-
The measure of angle
-
The measure of angle
-
The measure of angle
-
Write each expression with fewer terms.
- Find 44% of 625 using the facts that 40% of 625 is 250 and 4% of 625 is 25.
- What is 4.4% of 625?
- What is 0.44% of 625?