Lesson 15Distinguishing Volume and Surface Area
Let’s work with surface area and volume in context.
Learning Targets:
- I can decide whether I need to find the surface area or volume when solving a problem about a real-world situation.
15.1 The Science Fair
Mai’s science teacher told her that when there is more ice touching the water in a glass, the ice melts faster. She wants to test this statement so she designs her science fair project to determine if crushed ice or ice cubes will melt faster in a drink.
She begins with two cups of warm water. In one cup, she puts a cube of ice. In a second cup, she puts crushed ice with the same volume as the cube. What is your hypothesis? Will the ice cube or crushed ice melt faster, or will they melt at the same rate? Explain your reasoning.
15.2 Revisiting the Box of Chocolates
The other day, you calculated the volume of this heart-shaped box of chocolates.
The depth of the box is 2 inches. How much cardboard is needed to create the box?
15.3 Card Sort: Surface Area or Volume
Your teacher will give you cards with different figures and questions on them.
- Sort the cards into two groups based on whether it would make more sense to think about the surface area or the volume of the figure when answering the question. Pause here so your teacher can review your work.
- Your teacher will assign you a card to examine more closely. What additional information would you need to be able to answer the question on your card?
- Estimate reasonable measurements for the figure on your card.
-
Use your estimated measurements to calculate the answer to the question.
Are you ready for more?
A cake is shaped like a square prism. The top is 20 centimeters on each side, and the cake is 10 centimeters tall. It has frosting on the sides and on the top, and a single candle on the top at the exact center of the square. You have a knife and a 20-centimeter ruler.
- Find a way to cut the cake into 4 fair portions, so that all 4 portions have the same amount of cake and frosting.
- Find another way to cut the cake into 4 fair portions.
- Find a way to cut the cake into 5 fair portions.
15.4 A Wheelbarrow of Concrete
A wheelbarrow is being used to carry wet concrete. Here are its dimensions.
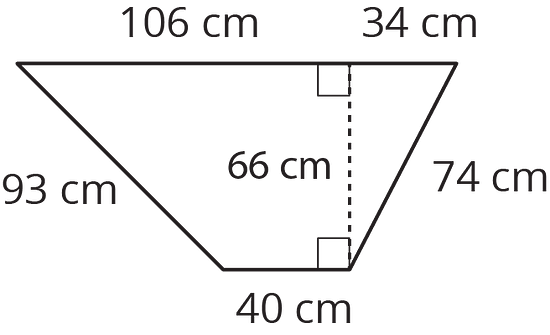
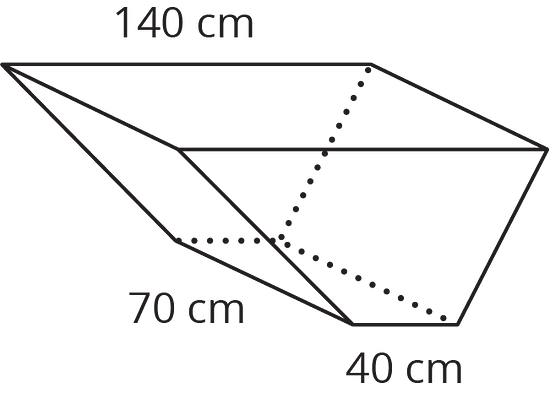
- What volume of concrete would it take to fill the tray?
- After dumping the wet concrete, you notice that a thin film is left on the inside of the tray. What is the area of the concrete coating the tray? (Remember, there is no top.)
Lesson 15 Summary
Sometimes we need to find the volume of a prism, and sometimes we need to find the surface area.
Here are some examples of quantities related to volume:
- How much water a container can hold
- How much material it took to build a solid object
Volume is measured in cubic units, like in3 or m3.
Here are some examples of quantities related to surface area:
- How much fabric is needed to cover a surface
- How much of an object needs to be painted
Surface area is measured in square units, like in2 or m2.
Lesson 15 Practice Problems
Here is the base of a prism.
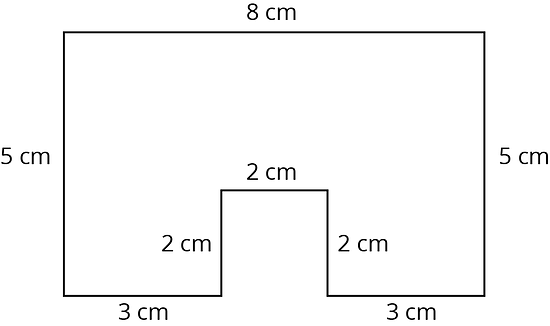
-
If the height of the prism is 5 cm, what is its surface area? What is its volume?
-
If the height of the prism is 10 cm, what is its surface area? What is its volume?
-
When the height doubled, what was the percent increase for the surface area? For the volume?
-
Select all the situations where knowing the volume of an object would be more useful than knowing its surface area.
-
Determining the amount of paint needed to paint a barn.
-
Determining the monetary value of a piece of gold jewelry.
-
Filling an aquarium with buckets of water.
-
Deciding how much wrapping paper a gift will need.
-
Packing a box with watermelons for shipping.
-
Charging a company for ad space on your race car.
-
Measuring the amount of gasoline left in the tank of a tractor.
-
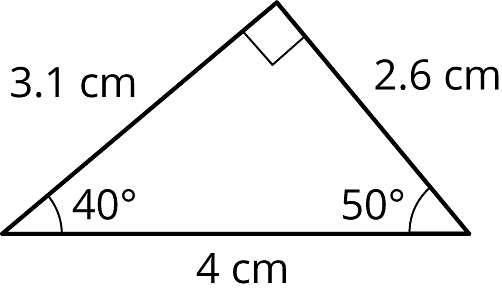
Han draws a triangle with a angle, a angle, and a side of length 4 cm as shown. Can you draw a different triangle with the same conditions?
Angle is half as large as angle . Angle is one fourth as large as angle . Angle has measure 240 degrees. What is the measure of angle ?
The Colorado state flag consists of three horizontal stripes of equal height. The side lengths of the flag are in the ratio . The diameter of the gold-colored disk is equal to the height of the center stripe. What percentage of the flag is gold?

“usa colorado flag clip art” via OpenClipArt. Public Domain.