Lesson 16Applying Volume and Surface Area
Let's explore things that are proportional to volume or surface area.
Learning Targets:
- I can solve problems involving the volume and surface area of children’s play structures.
16.1 You Decide
For each situation, decide if it requires Noah to calculate surface area or volume. Explain your reasoning.
-
Noah is planning to paint the bird house he built. He is unsure if he has enough paint.
-
Noah is planning to use a box with a trapezoid base to hold modeling clay. He is unsure if the clay will all fit in the box.
16.2 Foam Play Structure
At a daycare, Kiran sees children climbing on this foam play structure.
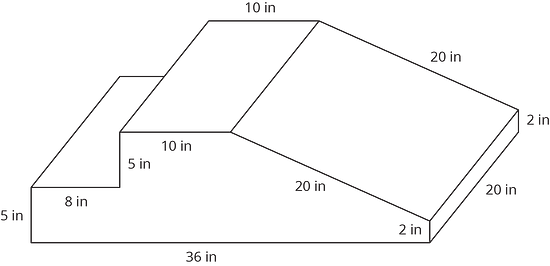
Kiran is thinking about building a structure like this for his younger cousins to play on.
- The entire structure is made out of soft foam so the children don’t hurt themselves. How much foam would Kiran need to build this play structure?
- The entire structure is covered with vinyl so it is easy to wipe clean. How much vinyl would Kiran need to build this play structure?
- The foam costs 0.8¢ per in3. Here is a table that lists the costs for different amounts of vinyl.
| vinyl (in2) | cost ($) |
|---|---|
| 75 | 0.45 |
| 125 | 0.75 |
What is the total cost for all the foam and vinyl needed to build this play structure?
Are you ready for more?
When he examines the play structure more closely, Kiran realizes it is really two separate pieces that are next to each other.
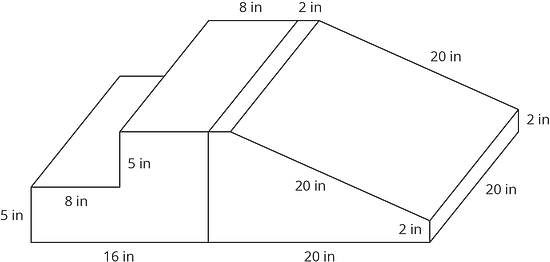
- How does this affect the amount of foam in the play structure?
-
How does this affect the amount of vinyl covering the play structure?
16.3 Filling the Sandbox
The daycare has two sandboxes that are both prisms with regular hexagons as their bases. The smaller sandbox has a base area of 1,146 in2 and is filled 10 inches deep with sand.
- It took 14 bags of sand to fill the small sandbox to this depth. What volume of sand comes in one bag? (Round to the nearest whole cubic inch.)
- The daycare manager wants to add 3 more inches to the depth of the sand in the small sandbox. How many bags of sand will they need to buy?
- The daycare manager also wants to add 3 more inches to the depth of the sand in the large sandbox. The base of the large sandbox is a scaled copy of the base of the small sandbox, with a scale factor of 1.5. How many bags of sand will they need to buy for the large sandbox?
-
A lawn and garden store is selling 6 bags of sand for $19.50. How much will they spend to buy all the new sand for both sandboxes?
Lesson 16 Summary
Suppose we wanted to make a concrete bench like the one shown in this picture. If we know that the finished bench has a volume of 10 ft3 and a surface area of 44 ft2 we can use this information to solve problems about the bench.
For example,
- How much does the bench weigh?
- How long does it take to wipe the whole bench clean?
- How much will the materials cost to build the bench and to paint it?
To figure out how much the bench weighs, we can use its volume, 10 ft3. Concrete weighs about 150 pounds per cubic foot, so this bench weighs about 1,500 pounds, because .
To figure out how long it takes to wipe the bench clean, we can use its surface area, 44 ft2. If it takes a person about 2 seconds per square foot to wipe a surface clean, then it would take about 88 seconds to clean this bench, because . It may take a little less than 88 seconds, since the surfaces where the bench is touching the ground do not need to be wiped.
Would you use the volume or the surface area of the bench to calculate the cost of the concrete needed to build this bench? And for the cost of the paint?
Lesson 16 Practice Problems
A landscape architect is designing a pool that has this top view:
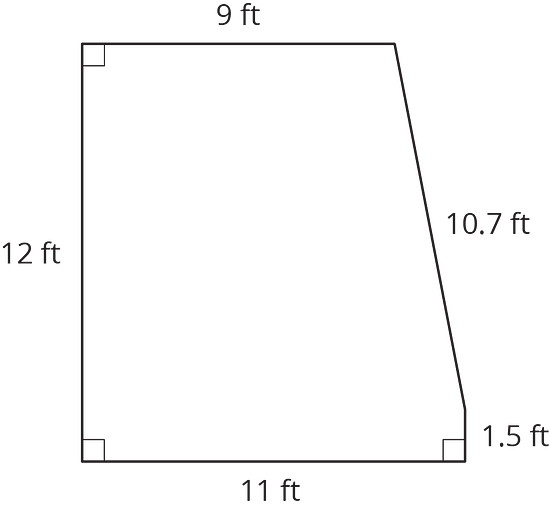
- How much water will be needed to fill this pool 4 feet deep?
- Before filling up the pool, it gets lined with a plastic liner. How much liner is needed for this pool?
- Here are the prices for different amounts of plastic liner. How much will all the plastic liner for the pool cost?
plastic liner (ft2) cost ($) 25 3.75 50 7.50 75 11.25
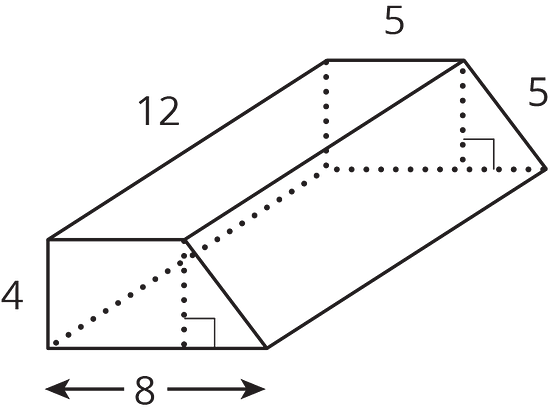
Shade in a base of the trapezoidal prism. (Be careful! The base is not the same as the bottom.)
- Find the area of the base you shaded.
- Find the volume of this trapezoidal prism.
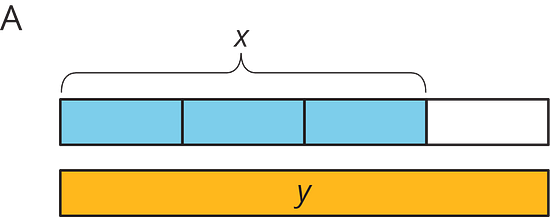
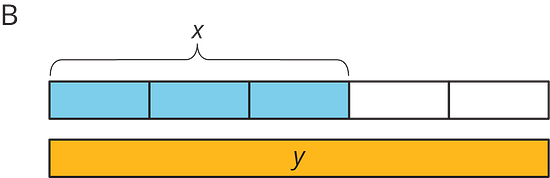
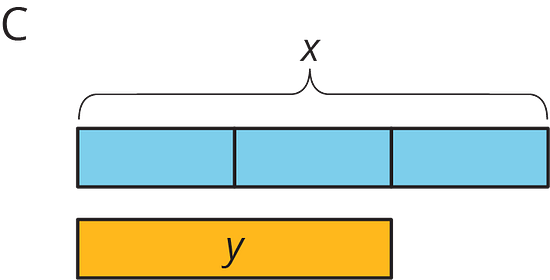
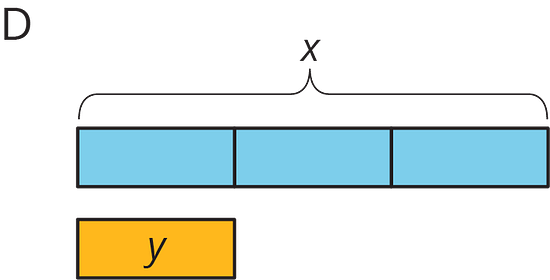
For each diagram, decide if is an increase or a decrease of . Then determine the percentage that increased or decreased to result in .
Noah is visiting his aunt in Texas. He wants to buy a belt buckle whose price is $25. He knows that the sales tax in Texas is 6.25%.
- How much will the tax be on the belt buckle?
- How much will Noah spend for the belt buckle including the tax?
- Write an equation that represents the total cost, , of an item whose price is .