Lesson 2Adjacent Angles
Let’s look at some special pairs of angles.
Learning Targets:
- I can find unknown angle measures by reasoning about complementary or supplementary angles.
- I can recognize when adjacent angles are complementary or supplementary.
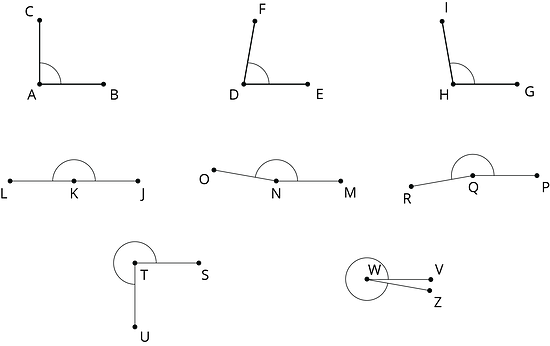
2.1 Estimating Angle Measures
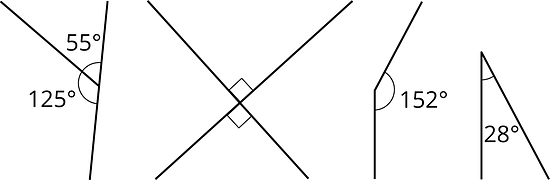
Estimate the degree measure of each indicated angle.
2.2 Cutting Rectangles
Your teacher will give you two small, rectangular papers.
- On one of the papers, draw a small half-circle in the middle of one side.

- Cut a straight line, starting from the center of the half-circle, all the way across the paper to make 2 separate pieces. (Your cut does not need to be perpendicular to the side of the paper.)
- On each of these two pieces, measure the angle that is marked by part of a circle. Label the angle measure on the piece.
- What do you notice about these angle measures?
- Clare measured 70 degrees on one of her pieces. Predict the angle measure of her other piece.
- On the other rectangular paper, draw a small quarter-circle in one of the corners.
- Repeat the previous steps to cut, measure, and label the two angles marked by part of a circle.

- What do you notice about these angle measures?
- Priya measured 53 degrees on one of her pieces. Predict the angle measure of her other piece.
2.3 Is It a Complement or Supplement?
-
Use the protractor in the picture to find the measure of angles:
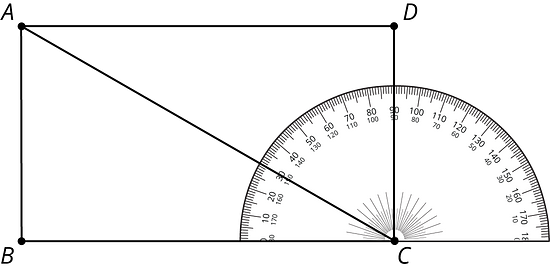
-
Explain how to find the measure of angle without repositioning the protractor.
-
Use the protractor in the picture to find the measure of angles:

-
Explain how to find the measure of angle without repositioning the protractor.
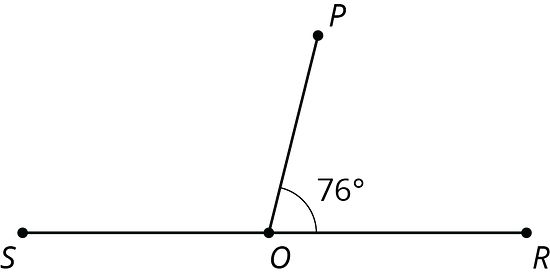
- Angle is a right angle. Find the measure of angle .

- Point is on line . Find the measure of angle .
Are you ready for more?
Clare started with a rectangular piece of paper. She folded up one corner, and then folded up the other corner, as shown in the photos.



- Try this yourself with any rectangular paper. Fold the left corner up at any angle, and then fold the right corner up so that the edges of the paper meet.
- Clare thought that the angle at the bottom looked like a 90 degree angle. Does yours also look like it is 90 degrees?
-
Can you explain why the bottom angle always has to be 90 degrees? Hint: the third photo shows Clare’s paper, unfolded. The crease marks have dashed lines, and the line where the two paper edges met have a solid line. Mark these on your own paper as well.
Lesson 2 Summary
If two angle measures add up to , then we say the angles are complementary. Here are three examples of pairs of complementary angles.
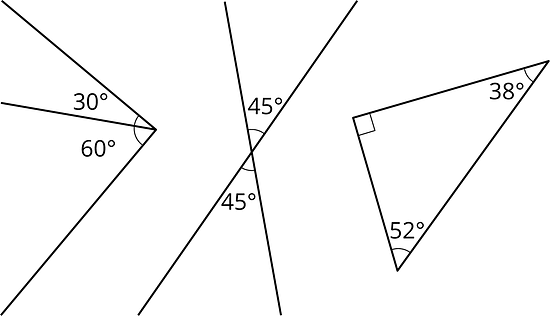
If two angle measures add up to , then we say the angles are supplementary. Here are three examples of pairs of supplementary angles.
Glossary Terms
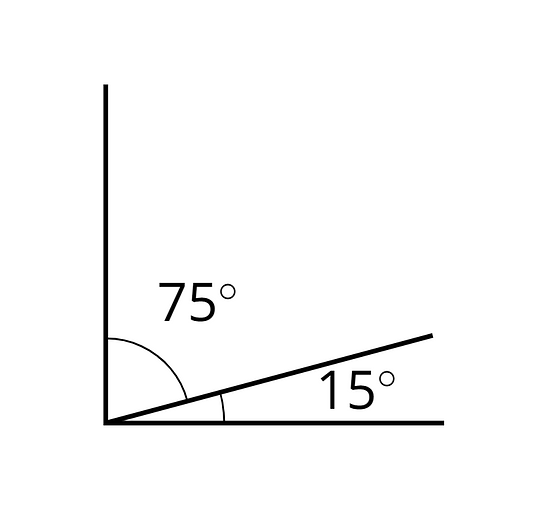
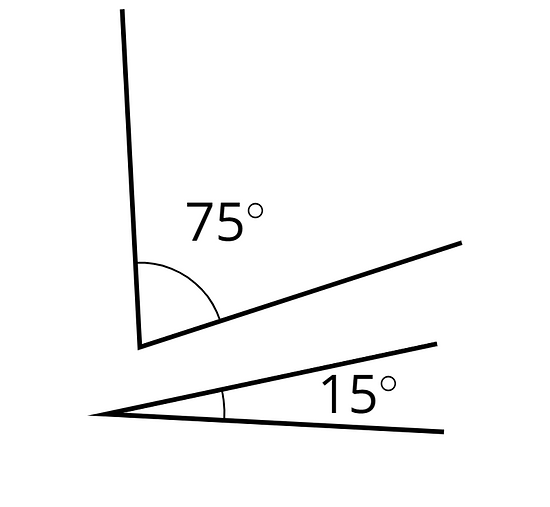
Complementary angles have measures that add up to 90 degrees.
For example, a angle and a angle are complementary.
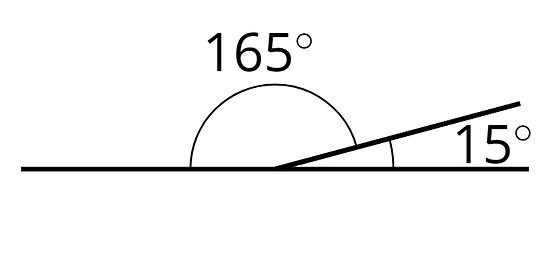
Supplementary angles have measures that add up to 180 degrees.
For example, a angle and a angle are supplementary.
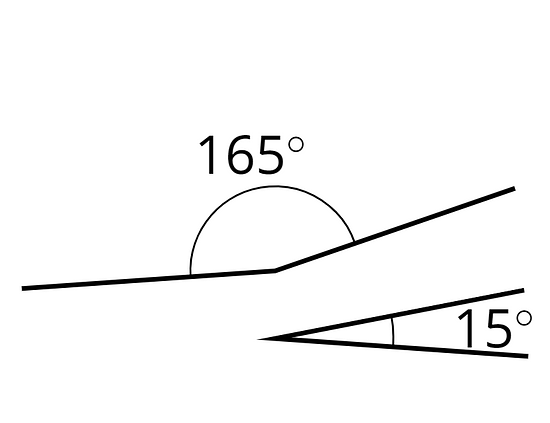
Lesson 2 Practice Problems
Angles and are supplementary. Find the measure of angle .
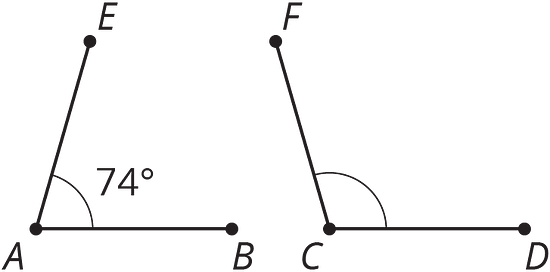
-
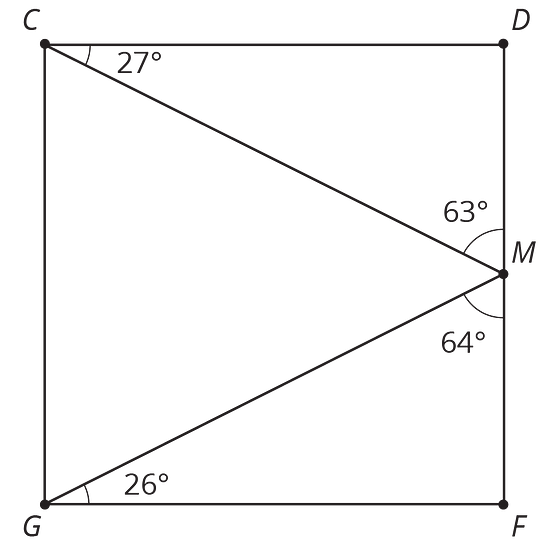
List two pairs of angles in square that are complementary.
- Name three angles that sum to .
-
Complete the equation with a number that makes the expression on the right side of the equal sign equivalent to the expression on the left side.
Match each table with the equation that represents the same proportional relationship.
-
2 8 3 12 4 16 5 20 -
3 4.5 6 9 7 10.5 10 15 -
2 4 5 6 12 15
-