Open Up Resources Logo

Lesson 16Parallel Lines and the Angles in a Triangle

Let’s see why the angles in a triangle add to 180 degrees.

Learning Targets:

  • I can explain using pictures why the sum of the angles in any triangle is 180 degrees.

16.1 True or False: Computational Relationships

Is each equation true or false?

62-28= 60-30

3\boldcdot \text{-}8= (2\boldcdot \text{-}8) - 8

\dfrac {16}{\text{-}2} + \dfrac{24}{\text{-}2} = \dfrac{40}{\text{-}2}

16.2 Angle Plus Two

Here is triangle ABC .

Select the Midpoint tool 

 and click on two points or a segment to find the midpoint.
open applet in presentation mode

  1. Rotate triangle ABC 180^\circ around the midpoint of side AC . Right click on the point and select Rename to label the new vertex D .

  2. Rotate triangle ABC 180^\circ around the midpoint of side AB . Right click on the point and select Rename to label the new vertex E .

  3. Look at angles EAB , BAC , and CAD . Without measuring, write what you think is the sum of the measures of these angles. Explain or show your reasoning.

  4. Is the measure of angle EAB equal to the measure of any angle in triangle ABC ? If so, which one? If not, how do you know?

  5. Is the measure of angle CAD equal to the measure of any angle in triangle ABC ? If so, which one? If not, how do you know?

  6. What is the sum of the measures of angles ABC , BAC , and ACB ?

16.3 Every Triangle in the World

Here is \triangle ABC . Line DE is parallel to line AC .

Triangle ABC is between two parallel lines.

  1. What is m{\angle DBA} + b + m{\angle CBE} ? Explain how you know.

  2. Use your answer to explain why a + b + c = 180 .

  3. Explain why your argument will work for any triangle: that is, explain why the sum of the angle measures in any triangle is 180^\circ .

Are you ready for more?

  1. Using a ruler, create a few quadrilaterals. Use a protractor to measure the four angles inside the quadrilateral. What is the sum of these four angle measures?

  2. Come up with an explanation for why anything you notice must be true (hint: draw one diagonal in each quadrilateral).

16.4 Four Triangles Revisited

This diagram shows a square BDFH that has been made by images of triangle ABC under rigid transformations.

Square BDFH is made up of 4 right triangles and Square ACEG.
Given that angle BAC measures 53 degrees, find as many other angle measures as you can.

Lesson 16 Summary

Using parallel lines and rotations, we can understand why the angles in a triangle always add to 180^\circ . Here is triangle ABC . Line DE is parallel to AC and contains B .

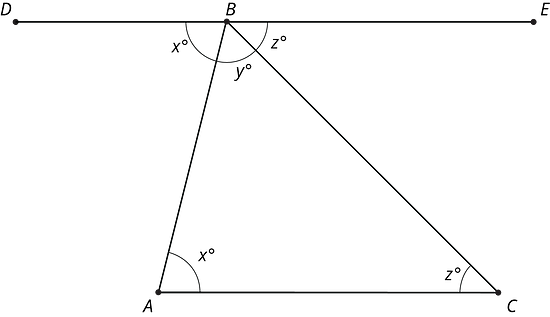
Triangle ABC has a tangent line of DE at point B. Angles are undetermined

A 180 degree rotation of triangle ABC around the midpoint of AB interchanges angles A and DBA so they have the same measure: in the picture these angles are marked as x^\circ . A 180 degree rotation of triangle ABC around the midpoint of BC interchanges angles C and CBE so they have the same measure: in the picture, these angles are marked as z^\circ . Also, DBE is a straight line because 180 degree rotations take lines to parallel lines. So the three angles with vertex  B make a line and they add up to 180^\circ  ( x + y + z = 180 ). But x, y, z are the measures of the three angles in \triangle ABC so the sum of the angles in a triangle is always 180^\circ !

Lesson 16 Practice Problems

  1. For each triangle, find the measure of the missing angle.

    Four triangles are shown all with different angles.

  2. Is there a triangle with two right angles? Explain your reasoning.

  3. In this diagram, lines AB and CD are parallel.

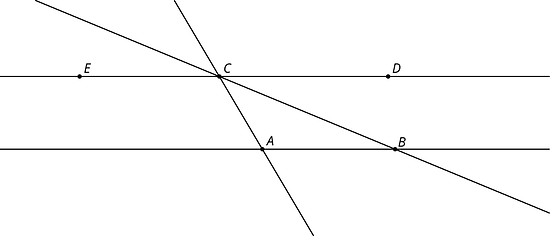
    Two parallel lines are itersected by two other lines.

    Angle ABC measures 35^\circ and angle BAC measures 115^\circ .

    1. What is m{\angle ACE} ?
    2. What is m{\angle DCB} ?
    3. What is m{\angle ACB} ?

  4. The two figures are congruent.

    1. Label the points A’ , B’ and C’ that correspond to A , B , and C in the figure on the right.
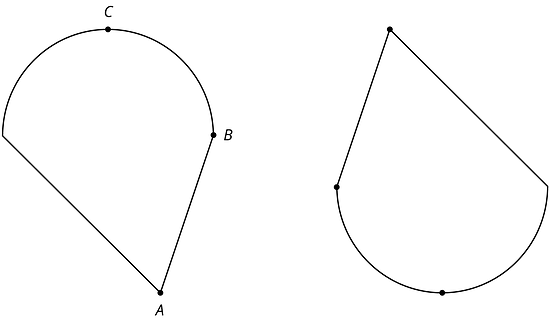
      Two congruent figures are shown
    2. If segment AB measures 2 cm, how long is segment A’B’ ? Explain.
    3. The point D is shown in addition to A and C . How can you find the point D’ that corresponds to D ? Explain your reasoning.
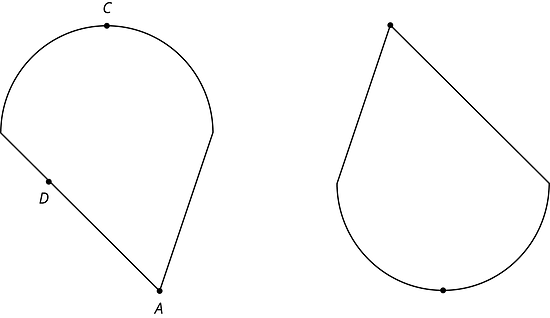
      Two congruent figures are shown