Open Up Resources Logo

Lesson 15Adding the Angles in a Triangle

Let’s explore angles in triangles.

Learning Targets:

  • If I know two of the angle measures in a triangle, I can find the third angle measure.

15.1 Can You Draw It?

  1. Complete the table by drawing a triangle in each cell that has the properties listed for its column and row. If you think you cannot draw a triangle with those properties, write “impossible” in the cell.

  2. Share your drawings with a partner. Discuss your thinking. If you disagree, work to reach an agreement.

acute (all angles acute) right (has a right angle) obtuse (has an obtuse angle)
scalene (side lengths all different)
isosceles (at least two side lengths are equal)
equilateral (three side lengths equal)

15.2 Find All Three

Your teacher will give you a card with a picture of a triangle.

  1. The measurement of one of the angles is labeled. Mentally estimate the measures of the other two angles.

  2. Find two other students with triangles congruent to yours but with a different angle labeled. Confirm that the triangles are congruent, that each card has a different angle labeled, and that the angle measures make sense.

  3. Enter the three angle measures for your triangle on the table your teacher has posted.

15.3 Tear It Up

Your teacher will give you a page with three sets of angles and a blank space. Cut out each set of three angles. Can you make a triangle from each set that has these same three angles?

Are you ready for more?

  1. Draw a quadrilateral. Cut it out, tear off its angles, and line them up. What do you notice?

  2. Repeat this for several more quadrilaterals. Do you have a conjecture about the angles?

Lesson 15 Summary

A 180^\circ angle is called a straight angle because when it is made with two rays, they point in opposite directions and form a straight line.

If we experiment with angles in a triangle, we find that the sum of the measures of the three angles in each triangle is 180^\circ —the same as a straight angle!

Through experimentation we find:

  • If we add the three angles of a triangle physically by cutting them off and lining up the vertices and sides, then the three angles form a straight angle.

  • If we have a line and two rays that form three angles added to make a straight angle, then there is a triangle with these three angles.

Glossary Terms

straight angle

A straight angle is an angle that forms a straight line. It measures 180 degrees.

Lesson 15 Practice Problems

  1. In triangle ABC , the measure of angle A is 40^\circ .

    1. Give possible measures for angles B and C if triangle ABC is isosceles.
    2. Give possible measures for angles B and C if triangle ABC is right.

  2. For each set of angles, decide if there is a triangle whose angles have these measures in degrees:

    1. 60, 60, 60
    2. 90, 90, 45
    3. 30, 40, 50
    4. 90, 45, 45
    5. 120, 30, 30

    If you get stuck, consider making a line segment. Then use a protractor to measure angles with the first two angle measures.

  3. Angle A in triangle ABC is obtuse. Can angle B or angle C be obtuse? Explain your reasoning.

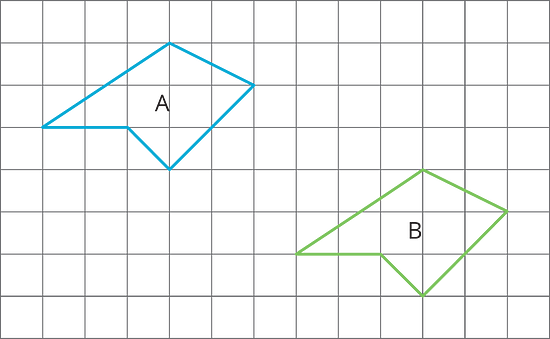
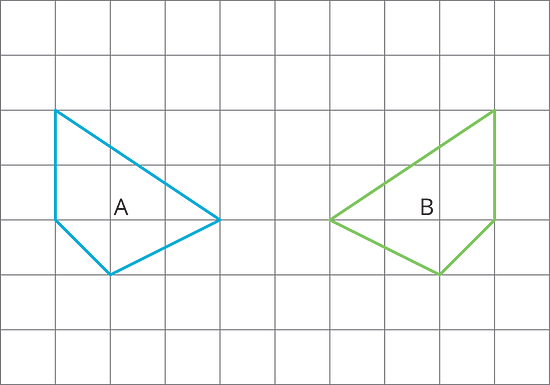
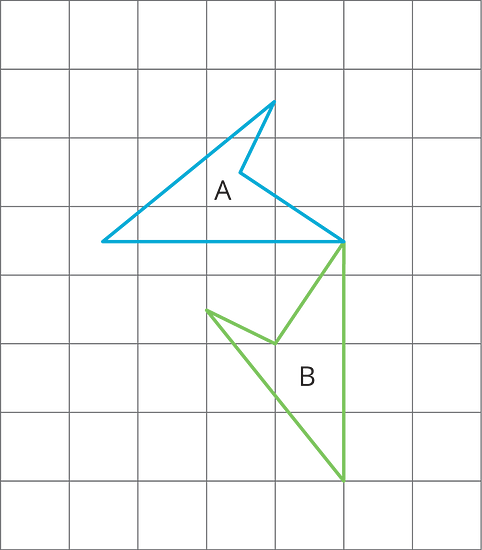
  4. For each pair of polygons, describe the transformation that could be applied to Polygon A to get Polygon B.

  5. On the grid, draw a scaled copy of quadrilateral ABCD using a scale factor of \frac12 .