Lesson 7No Bending or Stretching
Let’s compare measurements before and after translations, rotations, and reflections.
Learning Targets:
- I can describe the effects of a rigid transformation on the lengths and angles in a polygon.
7.1 Measuring Segments
For each question, the unit is represented by the large tick marks with whole numbers.
- Find the length of this segment to the nearest of a unit.
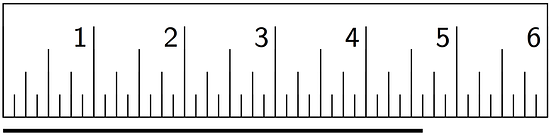
- Find the length of this segment to the nearest 0.1 of a unit.
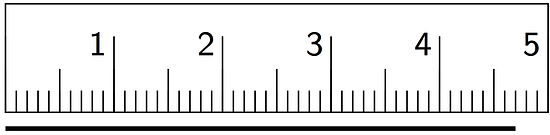
- Estimate the length of this segment to the nearest of a unit.
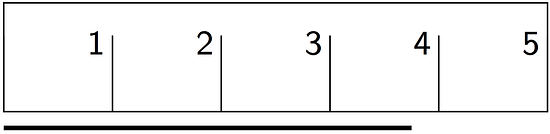
-
Estimate the length of the segment in the prior question to the nearest 0.1 of a unit.
7.2 Sides and Angles
- Translate Polygon so point goes to point . In the image, write in the length of each side, in grid units, next to the side using the draw tool.
- Rotate Triangle clockwise using as the center of rotation. In the image, write the measure of each angle in its interior using the draw tool.
- Reflect Pentagon across line .
- In the image, write the length of each side, in grid units, next to the side.
- In the image, write the measure of each angle in the interior.
7.3 Which One?
Here is a grid showing triangle and two other triangles.
You can use a rigid transformation to take triangle to one of the other triangles.
-
Which one? Explain how you know.
-
Describe a rigid transformation that takes to the triangle you selected.
Lesson 7 Summary
The transformations we’ve learned about so far, translations, rotations, reflections, and sequences of these motions, are all examples of rigid transformations. A rigid transformation is a move that doesn’t change measurements on any figure.
Earlier, we learned that a figure and its image have corresponding points. With a rigid transformation, figures like polygons also have corresponding sides and corresponding angles. These corresponding parts have the same measurements.
For example, triangle was made by reflecting triangle across a horizontal line, then translating. Corresponding sides have the same lengths, and corresponding angles have the same measures.
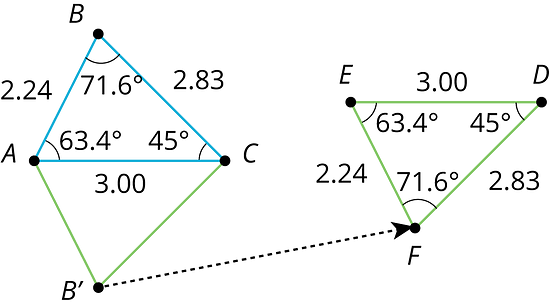
| measurements in triangle | corresponding measurements in image |
|---|---|
Glossary Terms
When part of an original figure matches up with part of a copy, we call them corresponding parts. These could be points, segments, angles, or distances.
For example, point in the first triangle corresponds to point in the second triangle.
Segment corresponds to segment .
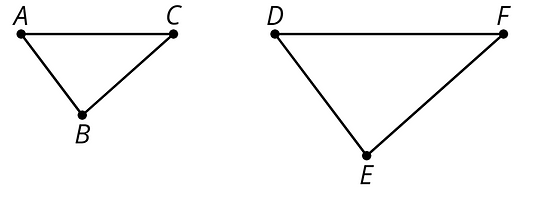
A rigid transformation is a move that does not change any measurements of a figure. Translations, rotations, and reflections are rigid transformations, as is any sequence of these.
Lesson 7 Practice Problems
Is there a rigid transformation taking Rhombus P to Rhombus Q? Explain how you know.
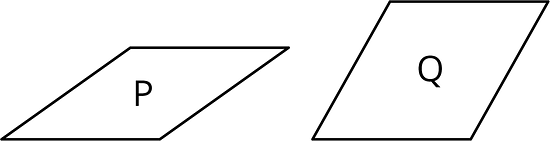
Describe a rigid transformation that takes Triangle A to Triangle B.

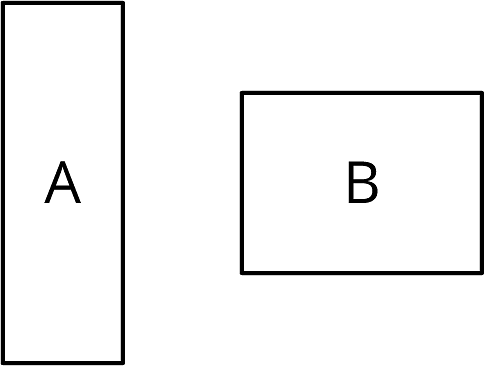
Is there a rigid transformation taking Rectangle A to Rectangle B? Explain how you know.
For each shape, draw its image after performing the transformation. If you get stuck, consider using tracing paper.
- Translate the shape so that goes to .

- Rotate the shape 180 degrees counterclockwise around .
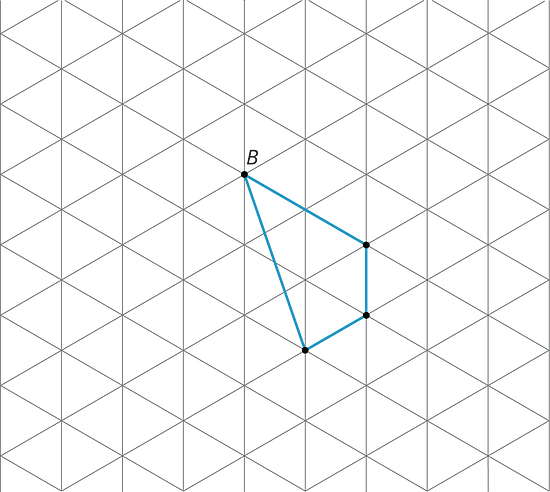
- Reflect the shape over the line shown.
