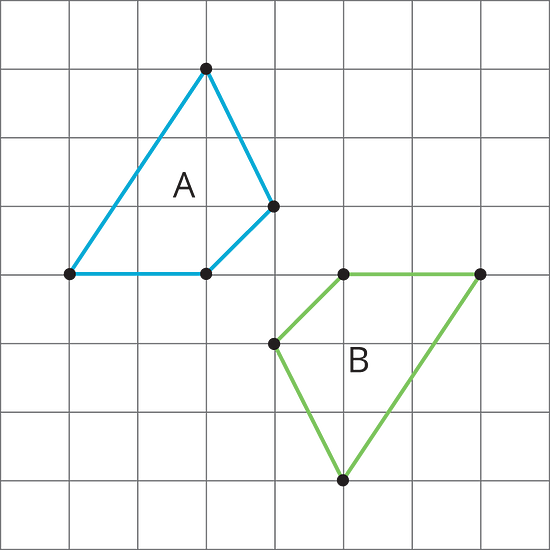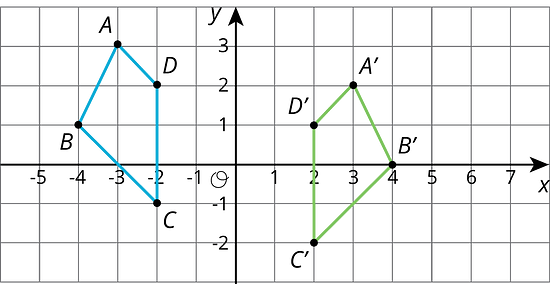Lesson 8Rotation Patterns
Let’s rotate figures in a plane.
Learning Targets:
- I can describe how to move one part of a figure to another using a rigid transformation.
8.1 Building a Quadrilateral
Here is a right isosceles triangle:
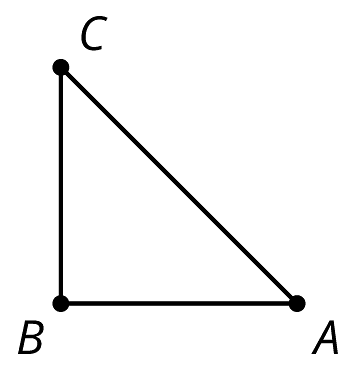
- Rotate triangle 90 degrees clockwise around .
- Rotate triangle 180 degrees clockwise around .
- Rotate triangle 270 degrees clockwise around .
-
What would it look like when you rotate the four triangles 90 degrees clockwise around ? 180 degrees? 270 degrees clockwise?
8.2 Rotating a Segment
Create a segment and a point that is not on segment .
-
Rotate segment around point .
-
Rotate segment around point .
Construct the midpoint of segment with the Midpoint tool.

-
Rotate segment around its midpoint. What is the image of A?
-
What happens when you rotate a segment ?
Are you ready for more?

8.3 A Pattern of Four Triangles
Here is a diagram built with three different rigid transformations of triangle .
Use the applet to answer the questions. It may be helpful to reset the image after each question.
- Describe a rigid transformation that takes triangle to triangle .
- Describe a rigid transformation that takes triangle to triangle .
- Describe a rigid transformation that takes triangle to triangle .
- Do segments , , , and all have the same length? Explain your reasoning.
Lesson 8 Summary
When we apply a 180-degree rotation to a line segment, there are several possible outcomes:
- The segment maps to itself (if the center of rotation is the midpoint of the segment).
- The image of the segment overlaps with the segment and lies on the same line (if the center of rotation is a point on the segment).
- The image of the segment does not overlap with the segment (if the center of rotation is not on the segment).
We can also build patterns by rotating a shape. For example, triangle shown here has . If we rotate triangle 60 degrees, 120 degrees, 180 degrees, 240 degrees, and 300 degrees clockwise, we can build a hexagon.
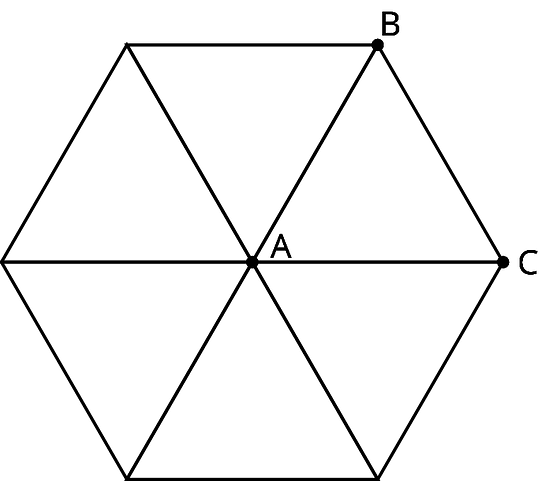
Lesson 8 Practice Problems
For the figure shown here,
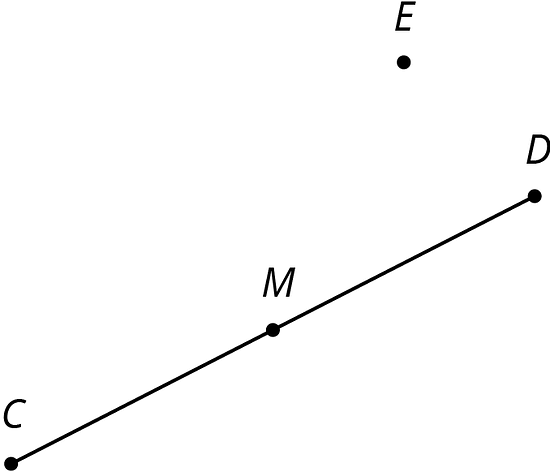
- Rotate segment around point .
- Rotate segment around point .
- Rotate segment around point .
Here is an isosceles right triangle:
Draw these three rotations of triangle together.
- Rotate triangle 90 degrees clockwise around .
- Rotate triangle 180 degrees around .
- Rotate triangle 270 degrees clockwise around .

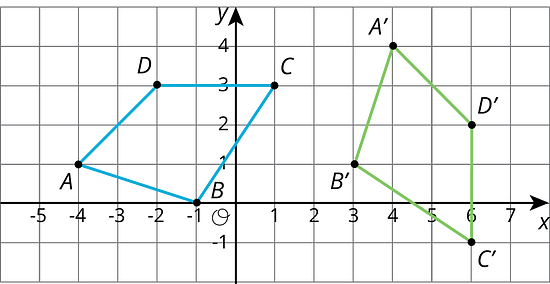
Each graph shows two polygons and . In each case, describe a sequence of transformations that takes to .
-
Lin says that she can map Polygon A to Polygon B using only reflections. Do you agree with Lin? Explain your reasoning.