Lesson 11Writing Equations for Lines
Let’s explore the relationship between points on a line and the slope of the line.
Learning Targets:
- I can decide whether a point is on a line by finding quotients of horizontal and vertical distances.
11.1 Coordinates and Lengths in the Coordinate Plane

Find each of the following and explain your reasoning:
- The length of segment .
- The coordinates of .
11.2 What We Mean by an Equation of a Line
Line is shown in the coordinate plane.
- What are the coordinates of and ?
-
Is point on line ? Explain how you know.
-
Is point on line ? Explain how you know.
-
Is point on line ? Explain how you know.
-
Suppose you know the - and -coordinates of a point. Write a rule that would allow you to test whether the point is on line .

11.3 Writing Relationships from Slope Triangles
Here are two diagrams:
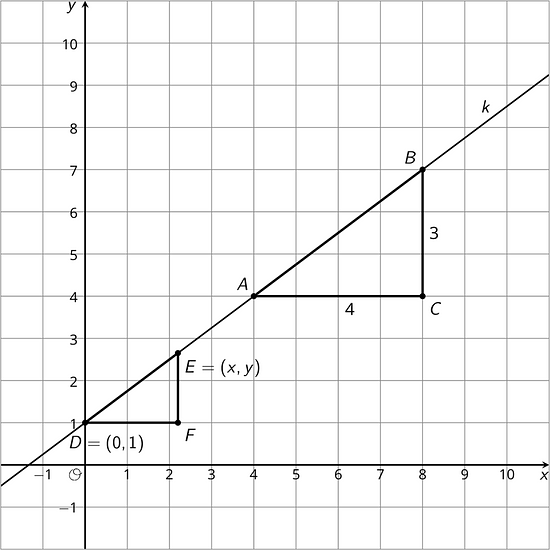

- Complete each diagram so that all vertical and horizontal segments have expressions for their lengths.
- Use what you know about similar triangles to find an equation for the quotient of the vertical and horizontal side lengths of in each diagram.
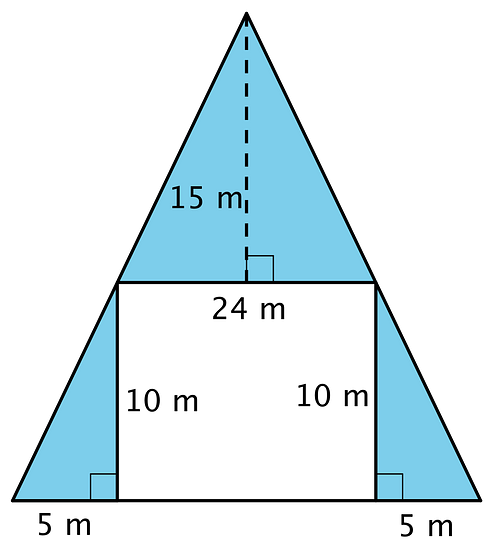
Are you ready for more?
- Find the area of the shaded region by summing the areas of the shaded triangles.
- Find the area of the shaded region by subtracting the area of the unshaded region from the large triangle.
- What is going on here?
Lesson 11 Summary
Here are the points , , and on the same line. Triangles and are slope triangles for the line so we know they are similar triangles. Let’s use their similarity to better understand the relationship between and , which make up the coordinates of point .

The slope for triangle is since the vertical side has length 2 and the horizontal side has length 1. The slope we find for triangle is because the vertical side has length and the horizontal side has length . These two slopes must be equal since they are from slope triangles for the same line, and so:
Since this means that the value of is twice the value of , or that . This equation is true for any point on the line!
Here are two different slope triangles. We can use the same reasoning to describe the relationship between and for this point .
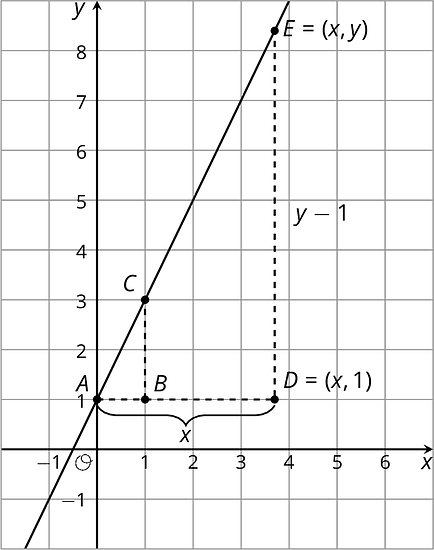
The slope for triangle is since the vertical side has length 2 and the horizontal side has length 1. For triangle , the horizontal side has length . The vertical side has length because the distance from to the -axis is but the vertical side of the triangle stops 1 unit short of the -axis. So the slope we find for triangle is . The slopes for the two slope triangles are equal, meaning:
Since is twice , another way to write this equation is . This equation is true for any point on the line!
Lesson 11 Practice Problems
For each pair of points, find the slope of the line that passes through both points. If you get stuck, try plotting the points on graph paper and drawing the line through them with a ruler.
- and
- and
- and
- and
Line is shown in the coordinate plane.

- What are the coordinates of and ?
- Is the point on line ? Explain how you know.
- Is the point on line ? Explain how you know.
- Is the point on line ? Explain how you know.
- Write a rule that would allow you to test whether is on line .
Consider the graphed line.
Mai uses Triangle A and says the slope of this line is . Elena uses Triangle B and says no, the slope of this line is 1.5. Do you agree with either of them? Explain.

A rectangle has length 6 and height 4.
Which of these would tell you that quadrilateral is definitely not similar to this rectangle? Select all that apply.