Lesson 12Using Equations for Lines
Let’s write equations for lines.
Learning Targets:
- I can find an equation for a line and use that to decide which points are on that line.
12.1 Missing center
A dilation with scale factor 2 sends to . Where is the center of the dilation?

12.2 Writing Relationships from Two Points
Here is a line.
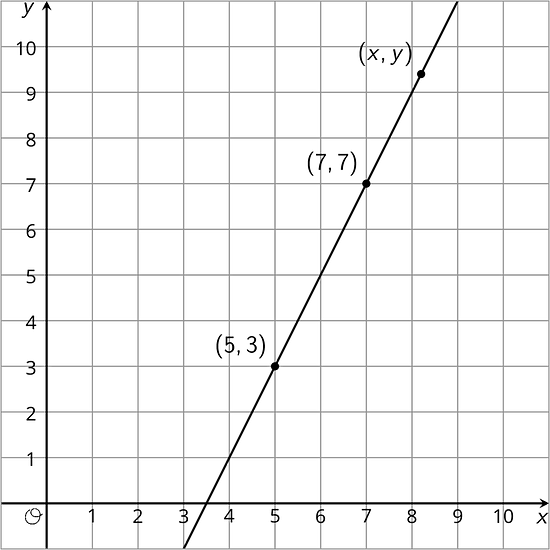
- Using what you know about similar triangles, find an equation for the line in the diagram.
- What is the slope of this line? Does it appear in your equation?
- Is also on the line? How do you know?
- Is also on the line?
Are you ready for more?
There are many different ways to write down an equation for a line like the one in the problem. Does represent the line? What about ? What about ? Explain your reasoning.
12.3 Dilations and Slope Triangles
Here is triangle .
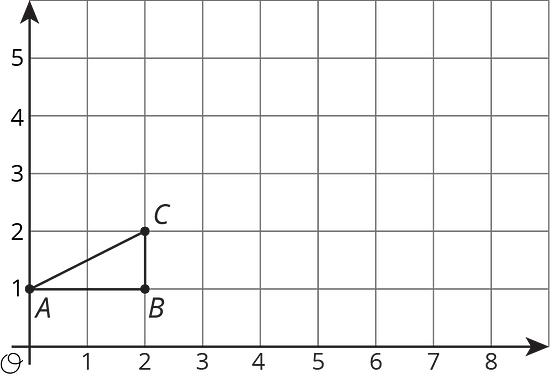
- Draw the dilation of triangle with center and scale factor 2.
- Draw the dilation of triangle with center and scale factor 2.5.
- Where is mapped by the dilation with center and scale factor ?
- For which scale factor does the dilation with center send to ? Explain how you know.
Lesson 12 Summary
We can use what we know about slope to decide if a point lies on a line. Here is a line with a few points labeled.

The slope triangle with vertices and gives a slope of . The slope triangle with vertices and gives a slope of . Since these slopes are the same, is an equation for the line. So, if we want to check whether or not the point lies on this line, we can check that . Since is a solution to the equation, it is on the line!
Lesson 12 Practice Problems
Select all the points that are on the line through and .
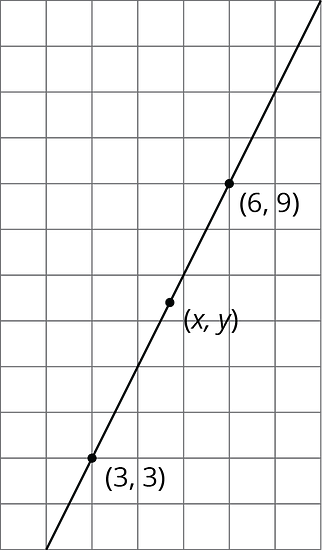
All three points displayed are on the line. Find an equation relating and .
Here is triangle .
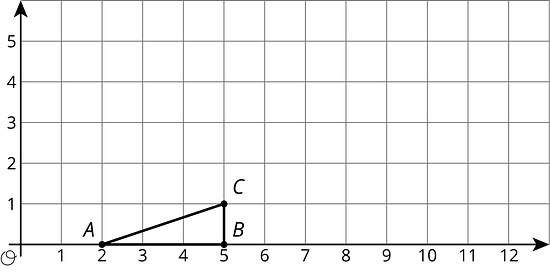
- Draw the dilation of triangle with center and scale factor 2.
- Draw the dilation of triangle with center and scale factor 3.
- Draw the dilation of triangle with center and scale factor .
- What are the coordinates of the image of point when triangle is dilated with center and scale factor ?
- Write an equation for the line containing all possible images of point .
Here are some line segments.

- Which segment is a dilation of using as the center of dilation and a scale factor of ?
- Which segment is a dilation of using as the center of dilation and a scale factor of ?
- Which segment is not a dilation of , and how do you know?