Lesson 2Keeping the Equation Balanced
Let's figure out unknown weights on balanced hangers.
Learning Targets:
- I can add or remove blocks from a hanger and keep the hanger balanced.
- I can represent balanced hangers with equations.
2.1 Notice and Wonder: Hanging Socks
What do you notice? What do you wonder?

2.2 Hanging Blocks
This picture represents a hanger that is balanced because the weight on both sides is the same.
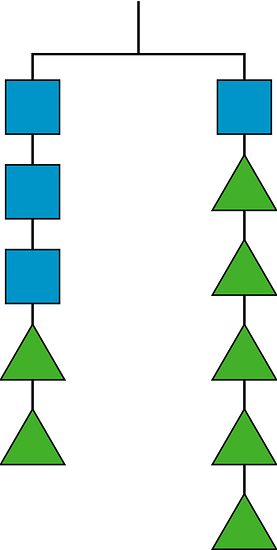
-
Elena takes two triangles off of the left side and three triangles off of the right side. Will the hanger still be in balance, or will it tip to one side? Which side? Explain how you know.
-
Use the applet to see if your answer to question [1] was correct. Can you find another way to make the hanger balance?
- If a triangle weighs 1 gram, how much does a square weigh? After you make a prediction, use the applet to see if you were right. Can you find another pair of values that makes the hanger balance?
Are you ready for more?
Try your own Hanger Balances!
2.3 More Hanging Blocks
- A triangle weighs 3 grams, and a circle weighs 6 grams.
-
Find the weight of a square.
-
A triangle weighs 3 grams, and a circle weighs 6 grams. Find the weight of a pentagon.
-
-
Write an equation to represent each hanger.
Are you ready for more?
Try your own!
Lesson 2 Summary
If we have equal weights on the ends of a hanger, then the hanger will be in balance. If there is more weight on one side than the other, the hanger will tilt to the heavier side.
We can think of a balanced hanger as a metaphor for an equation. An equation says that the expressions on each side have equal value, just like a balanced hanger has equal weights on each side.
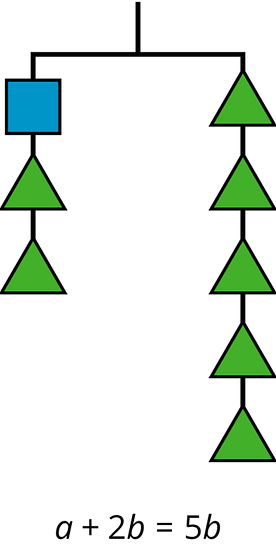
If we have a balanced hanger and add or remove the same amount of weight from each side, the result will still be in balance.
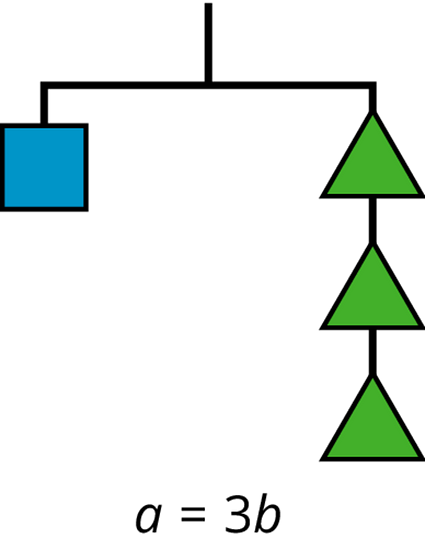
We can do these moves with equations as well: adding or subtracting the same amount from each side of an equation maintains the equality.
Lesson 2 Practice Problems
Which of the changes would keep the hanger in balance? Select all that apply.
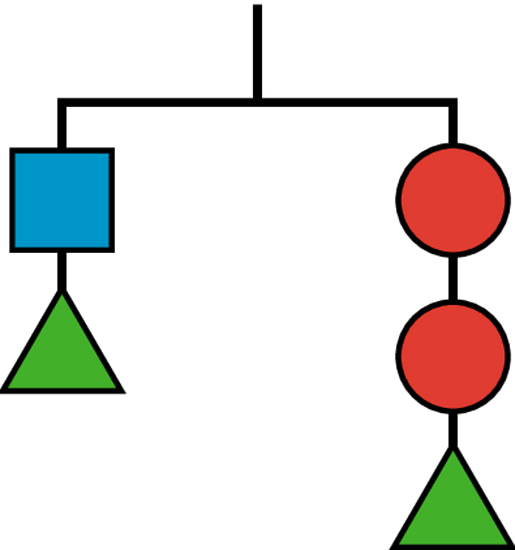
-
Adding two circles on the left and a square on the right
-
Adding 2 triangles to each side
-
Adding two circles on the right and a square on the left
-
Adding a circle on the left and a square on the right
-
Adding a triangle on the left and a square on the right
-
Here is a balanced hanger diagram.
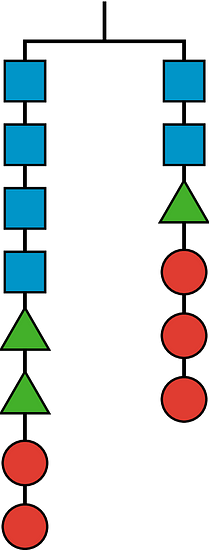
Each triangle weighs 2.5 pounds, each circle weighs 3 pounds, and represents the weight of each square. Select all equations that represent the hanger.
What is the weight of a square if a triangle weighs 4 grams?
Explain your reasoning.
Andre came up with the following puzzle. “I am three years younger than my brother, and I am 2 years older than my sister. My mom's age is one less than three times my brother's age. When you add all our ages, you get 87. What are our ages?”
-
Try to solve the puzzle.
-
Jada writes this equation for the sum of the ages: . Explain the meaning of the variable and each term of the equation.
-
Write the equation with fewer terms.
-
Solve the puzzle if you haven’t already.
-
These two lines are parallel. Write an equation for each.
