Lesson 3Balanced Moves
Let's rewrite equations while keeping the same solutions.
Learning Targets:
- I can add, subtract, multiply, or divide each side of an equation by the same expression to get a new equation with the same solution.
3.1 Matching Hangers
Figures A, B, C, and D show the result of simplifying the hanger in Figure A by removing equal weights from each side.

Here are some equations. Each equation represents one of the hanger diagrams.
-
Write the equation that goes with each figure:
A:
B:
C:
D: - Each variable (, , and ) represents the weight of one shape. Which goes with which?
- Explain what was done to each equation to create the next equation. If you get stuck, think about how the hangers changed.
3.2 Matching Equation Moves
Your teacher will give you some cards. Each of the cards 1 through 6 show two equations. Each of the cards A through E describe a move that turns one equation into another.
- Match each number card with a letter card.
- One of the letter cards will not have a match. For this card, write two equations showing the described move.
3.3 Keeping Equality
- Noah and Lin both solved the equation .
Do you agree with either of them? Why?
Noah's solution:
Lin's solution:
- Elena is asked to solve . What do you recommend she does to each side first?
- Diego is asked to solve . What do you recommend he does to each side first?
Are you ready for more?
In a cryptarithmetic puzzle, the digits 0–9 are represented with letters of the alphabet. Use your understanding of addition to find which digits go with the letters A, B, E, G, H, L, N, and R.
HANGER + HANGER + HANGER = ALGEBRA
Lesson 3 Summary
An equation tells us that two expressions have equal value. For example, if and have equal value, we can write the equation
Earlier, we used hangers to understand that if we add the same positive number to each side of the equation, the sides will still have equal value. It also works if we add negative numbers! For example, we can add -9 to each side of the equation.
Since expressions represent numbers, we can also add expressions to each side of an equation. For example, we can add to each side and still maintain equality.
If we multiply or divide the expressions on each side of an equation by the same number, we will also maintain the equality (so long as we do not divide by zero).
or
Now we can see that is the solution to our equation.
We will use these moves in systematic ways to solve equations in future lessons.
Lesson 3 Practice Problems
In this hanger, the weight of the triangle is and the weight of the square is .
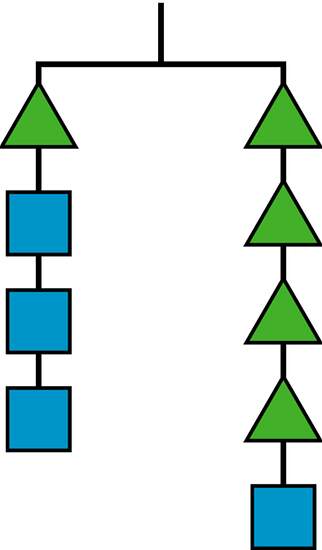
-
Write an equation using and to represent the hanger.
-
If is 6, what is ?
-
Match each set of equations with the move that turned the first equation into the second.
- Multiply both sides by
- Multiply both sides by
- Multiply both sides by
- Add to both sides
- Add to both sides
Andre and Diego were each trying to solve . Describe the first step they each make to the equation.
- The result of Andre’s first step was .
- The result of Diego’s first step was .
-
Complete the table with values for or that make this equation true: .
2 6 0 3 3 0 8 -
Create a graph, plot these points, and find the slope of the line that goes through them.

-
Select all the situations for which only zero or positive solutions make sense.
- Measuring temperature in degrees Celsius at an Arctic outpost each day in January.
- The height of a candle as it burns over an hour.
- The elevation above sea level of a hiker descending into a canyon.
- The number of students remaining in school after 6:00 p.m.
- A bank account balance over a year.
- The temperature in degrees Fahrenheit of an oven used on a hot summer day.