Lesson 14Finding Cylinder Dimensions
Let’s figure out the dimensions of cylinders.
Learning Targets:
- I can find missing information about a cylinder if I know its volume and some other information.
14.1 A Cylinder of Unknown Height
What is a possible volume for this cylinder if the diameter is 8 cm? Explain your reasoning.
14.2 What’s the Dimension?
The volume of a cylinder with radius is given by the formula .
- The volume of this cylinder with radius 5 units is cubic units. This statement is true:
What does the height of this cylinder have to be? Explain how you know.
- The volume of this cylinder with height 4 units is cubic units. This statement is true:
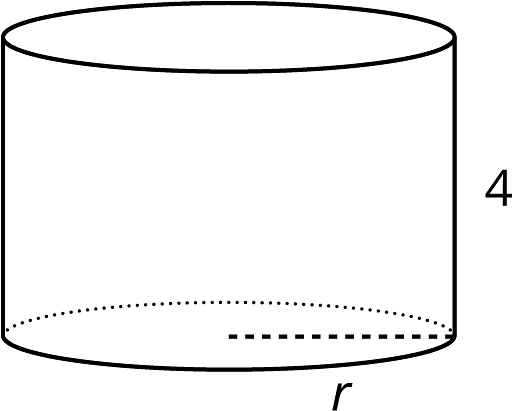
What does the radius of this cylinder have to be? Explain how you know.
Are you ready for more?
Suppose a cylinder has a volume of cubic inches, but it is not the same cylinder as the one you found earlier in this activity.
- What are some possibilities for the dimensions of the cylinder?
- How many different cylinders can you find that have a volume of cubic inches?
14.3 Cylinders with Unknown Dimensions
Each row of the table has information about a particular cylinder. Complete the table with the missing dimensions.
| diameter (units) | radius (units) | area of the base (square units) | height (units) | volume (cubic units) |
|---|---|---|---|---|
| 3 | 5 | |||
| 12 | ||||
| 11 | ||||
| 8 | ||||
| 100 | ||||
| 10 | ||||
| 20 | 314 | |||
Lesson 14 Summary
In an earlier lesson we learned that the volume, , of a cylinder with radius and height is
We say that the volume depends on the radius and height, and if we know the radius and height, we can find the volume. It is also true that if we know the volume and one dimension (either radius or height), we can find the other dimension.
For example, imagine a cylinder that has a volume of cm3 and a radius of 5 cm, but the height is unknown. From the volume formula we know that
must be true. Looking at the structure of the equation, we can see that . That means that the height has to be 20 cm, since .
Now imagine another cylinder that also has a volume of cm3 with an unknown radius and a height of 5 cm. Then we know that
must be true. Looking at the structure of this equation, we can see that . So the radius must be 10 cm.
Lesson 14 Practice Problems
Complete the table with all of the missing information about three different cylinders.
diameter of base (units) area of base (square units) height (units) volume (cubic units) 4 10 6 6 A cylinder has volume and radius 3. What is its height?
Three cylinders have a volume of 2826 cm3. Cylinder A has a height of 900 cm. Cylinder B has a height of 225 cm. Cylinder C has a height of 100 cm. Find the radius of each cylinder. Use 3.14 as an approximation for .
A gas company’s delivery truck has a cylindrical tank that is 14 feet in diameter and 40 feet long.
-
Sketch the tank, and mark the radius and the height.
-
How much gas can fit in the tank?
-
Here is a graph that shows the water height of the ocean between September 22 and September 24, 2016 in Bodega Bay, CA.
-
Estimate the water height at 12 p.m. on September 22.
-
How many times was the water height 5 feet? Find two times when this happens.
-
What was the lowest the water got during this time period? When does this occur?
-
Does the water ever reach a height of 6 feet?
-