Lesson 15The Volume of a Cone
Let’s explore cones and their volumes.
Learning Targets:
- I can find the volume of a cone in mathematical and real-world situations.
- I know the formula for the volume of a cone.
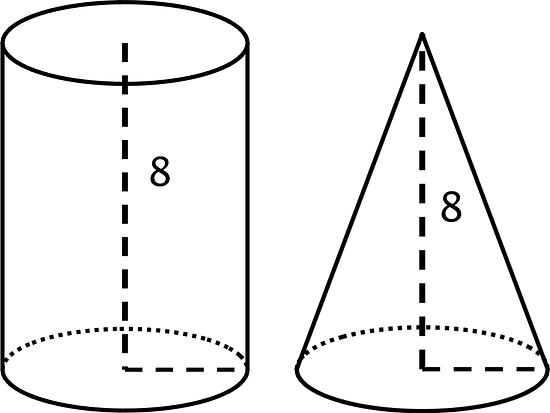
15.1 Which Has a Larger Volume?
The cone and cylinder have the same height, and the radii of their bases are equal.
- Which figure has a larger volume?
- Do you think the volume of the smaller one is more or less than the volume of the larger one? Explain your reasoning.
- Here is a method for quickly sketching a cone:
- Draw an oval.
- Draw a point centered above the oval.
- Connect the edges of the oval to the point.
- Which parts of your drawing would be hidden behind the object? Make these parts dashed lines.
15.2 From Cylinders to Cones
A cone and cylinder have the same height and their bases are congruent circles.
- If the volume of the cylinder is 90 cm3, what is the volume of the cone?
- If the volume of the cone is 120 cm3, what is the volume of the cylinder?
- If the volume of the cylinder is , what is the volume of the cone? Either write an expression for the cone or explain the relationship in words.
15.3 Calculate That Cone
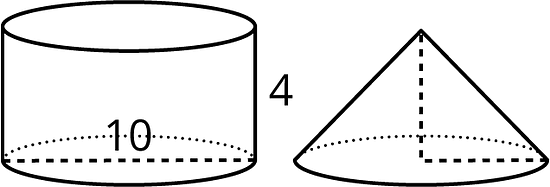
- Here is a cylinder and cone that have the same height and the same base area.
What is the volume of each figure? Express your answers in terms of .
- Here is a cone.
- What is the area of the base? Express your answer in terms of .
- What is the volume of the cone? Express your answer in terms of .
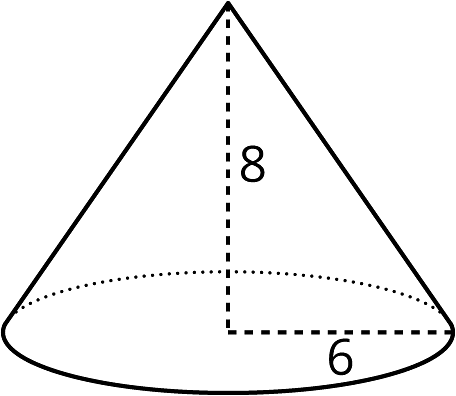
- A cone-shaped popcorn cup has a radius of 5 centimeters and a height of 9 centimeters. How many cubic centimeters of popcorn can the cup hold? Use 3.14 as an approximation for , and give a numerical answer.
Are you ready for more?
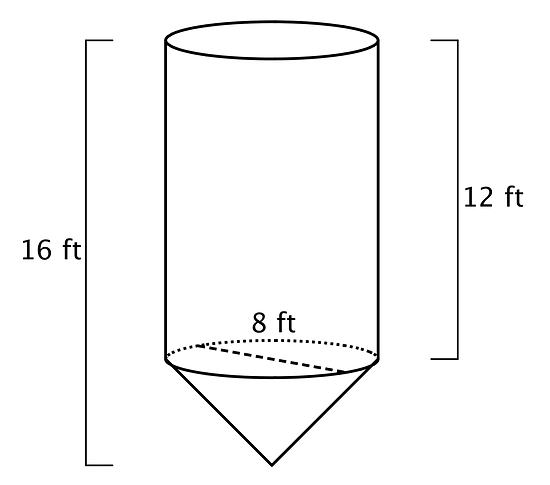
A grain silo has a cone shaped spout on the bottom in order to regulate the flow of grain out of the silo. The diameter of the silo is 8 feet. The height of the cylindrical part of the silo above the cone spout is 12 feet while the height of the entire silo is 16 feet.
How many cubic feet of grain are held in the cone spout of the silo? How many cubic feet of grain can the entire silo hold?
Lesson 15 Summary
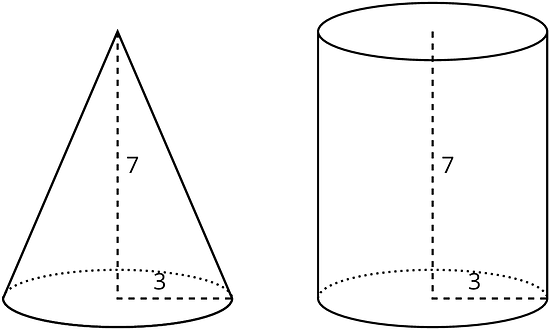
If a cone and a cylinder have the same base and the same height, then the volume of the cone is of the volume of the cylinder. For example, the cylinder and cone shown here both have a base with radius 3 feet and a height of 7 feet.
The cylinder has a volume of cubic feet since . The cone has a volume that is of that, or cubic feet.
If the radius for both is and the height for both is , then the volume of the cylinder is . That means that the volume, , of the cone is
Lesson 15 Practice Problems
A cylinder and cone have the same height and radius. The height of each is 5 cm, and the radius is 2 cm. Calculate the volume of the cylinder and the cone.
The volume of this cone is cubic units.
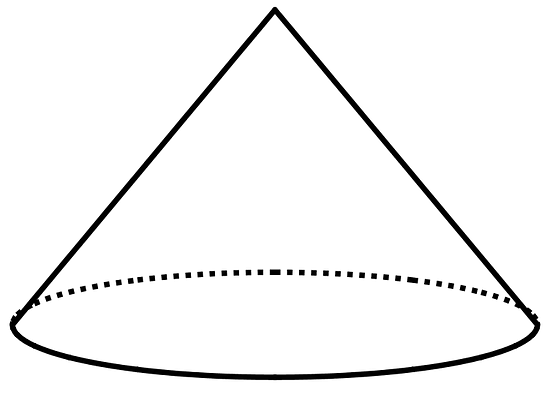
What is the volume of a cylinder that has the same base area and the same height?
A cylinder has a diameter of 6 cm and a volume of cm3.
- Sketch the cylinder.
- Find its height and radius in centimeters.
- Label your sketch with the cylinder’s height and radius.
Lin wants to get some custom T-shirts printed for her basketball team. Shirts cost $10 each if you order 10 or fewer shirts and $9 each if you order 11 or more shirts.
-
Make a graph that shows the total cost of buying shirts, for 0 through 15 shirts.
-
There are 10 people on the team. Do they save money if they buy an extra shirt? Explain your reasoning.
-
What is the slope of the graph between 0 and 10? What does it mean in the story?
-
What is the slope of the graph between 11 and 15? What does it mean in the story?
-
In the following graphs, the horizontal axis represents time and the vertical axis represents distance from school. Write a possible story for each graph.