Lesson 18Scaling Two Dimensions
Let’s change more dimensions of shapes.
Learning Targets:
- I can create a graph representing the relationship between volume and radius for all cylinders (or cones) with a fixed height.
- I can explain in my own words why changing the radius by a scale factor changes the volume by the scale factor squared.
18.1 Tripling Statements
, , , , and all represent positive integers. Consider these two equations:
- Which of these statements are true? Select all that apply.
- If is tripled, is tripled.
- If , , and are all tripled, then is tripled.
- If is tripled, is tripled.
- If , , and are all tripled, then is tripled.
- Create a true statement of your own about one of the equations.
18.2 A Square Base
Clare sketches a rectangular prism with a height of 11 and a square base and labels the edges of the base . She asks Han what he thinks will happen to the volume of the rectangular prism if she triples .
Are you ready for more?
A cylinder can be constructed from a piece of paper by curling it so that you can glue together two opposite edges (the dashed edges in the figure).
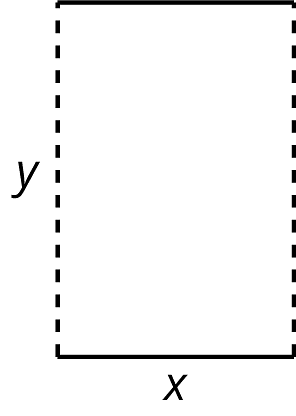
- If you wanted to increase the volume inside the resulting cylinder, would it make more sense to double , , or does it not matter?
- If you wanted to increase the surface area of the resulting cylinder, would it make more sense to double , , or does it not matter?
- How would your answers to these questions change if we made a cylinder by gluing together the solid lines instead of the dashed lines?
18.3 Playing with Cones
There are many cones with a height of 7 units. Let represent the radius and represent the volume of these cones.
- Write an equation that expresses the relationship between and . Use 3.14 as an approximation for .
- Predict what will happen to the volume if you triple the value of .
-
Graph this equation.
open applet in presentation mode2powered bypowered byxyaafunctionsaA B C - What happens to the volume if you triple ? Where do you see this in the graph? How can you see it algebraically?
Lesson 18 Summary
There are many rectangular prisms that have a length of 4 units and width of 5 units but differing heights. If represents the height, then the volume of such a prism is
The equation shows us that the volume of a prism with a base area of 20 square units is a linear function of the height. Because this is a proportional relationship, if the height gets multiplied by a factor of , then the volume is also multiplied by a factor of :
What happens if we scale two dimensions of a prism by a factor of ? In this case, the volume gets multiplied by a factor of twice, or .
For example, think about a prism with a length of 4 units, width of 5 units, and height of 6 units. Its volume is 120 cubic units since . Now imagine the length and width each get scaled by a factor of , meaning the new prism has a length of , width of , and a height of 6. The new volume is cubic units since .
A similar relationship holds for cylinders. Think of a cylinder with a height of 6 and a radius of 5. The volume would be cubic units since . Now, imagine the radius is scaled by a factor of . Then the new volume is or cubic units. So scaling the radius by a factor of has the effect of multiplying the volume by !
Why does the volume multiply by when only the radius changes? This makes sense if we imagine how scaling the radius changes the base area of the cylinder. As the radius increases, the base area gets larger in two dimensions (the circle gets wider and also taller), while the third dimension of the cylinder, height, stays the same.
Lesson 18 Practice Problems
There are many cylinders with a height of 18 meters. Let represent the radius in meters and represent the volume in cubic meters.
-
Write an equation that represents the volume as a function of the radius .
-
Complete this table, giving three possible examples.
1 -
If the radius of a cylinder is doubled, does the volume double? Explain how you know.
-
Is the graph of this function a line? Explain how you know.
-
As part of a competition, Diego must spin around in a circle 6 times and then run to a tree. The time he spends on each spin is represented by and the time he spends running is . He gets to the tree 21 seconds after he starts spinning.
- Write an equation showing the relationship between and .
- Rearrange the equation so that it shows as a function of .
- If it takes Diego 1.2 seconds to spin around each time, how many seconds did he spend running?
The table and graph represent two functions. Use the table and graph to answer the questions.
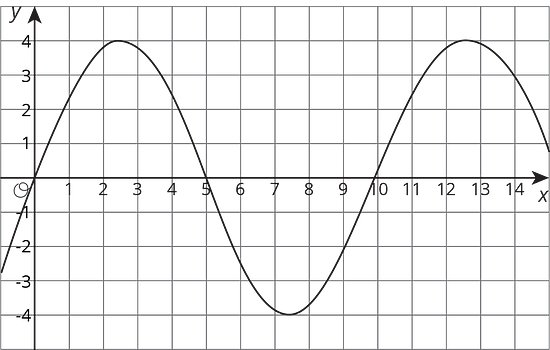
1 2 3 4 5 6 3 -1 0 4 5 -1 - For which values of is the output from the table less than the output from the graph?
- In the graphed function, which values of give an output of 0?
A cone has a radius of 3 units and a height of 4 units.
-
What is this volume of this cone?
-
Another cone has quadruple the radius, and the same height. How many times larger is the new cone’s volume?
-