Lesson 19Estimating a Hemisphere
Let’s estimate volume of hemispheres with figures we know.
Learning Targets:
- I can estimate the volume of a hemisphere by calculating the volume of shape I know is larger and the volume of a shape I know is smaller.
19.1 Notice and Wonder: Two Shapes
Here are two shapes.
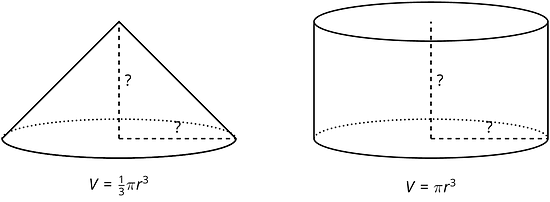
What do you notice? What do you wonder?
19.2 Hemispheres in Boxes
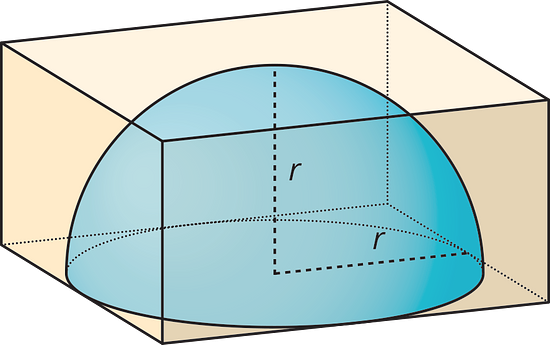
- Mai has a dome paperweight that she can use as a magnifier. The paperweight is shaped like a hemisphere made of solid glass, so she wants to design a box to keep it in so it won't get broken. Her paperweight has a radius of 3 cm.
- What should the dimensions of the inside of box be so the box is as small as possible?
- What is the volume of the box?
- What is a reasonable estimate for the volume of the paperweight?
- Tyler has a different box with side lengths that are twice as long as the sides of Mai's box. Tyler's box is just large enough to hold a different glass paperweight.
- What is the volume of the new box?
- What is a reasonable estimate for the volume of this glass paperweight?
- How many times bigger do you think the volume of the paperweight in this box is than the volume of Mai's paperweight? Explain your thinking.
19.3 Estimating Hemispheres
- A hemisphere with radius 5 units fits snugly into a cylinder of the same radius and height.
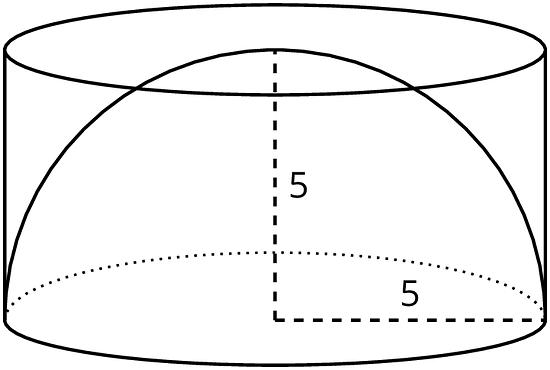
- Calculate the volume of the cylinder.
- Estimate the volume of the hemisphere. Explain your reasoning.
- A cone fits snugly inside a hemisphere, and they share a radius of 5.
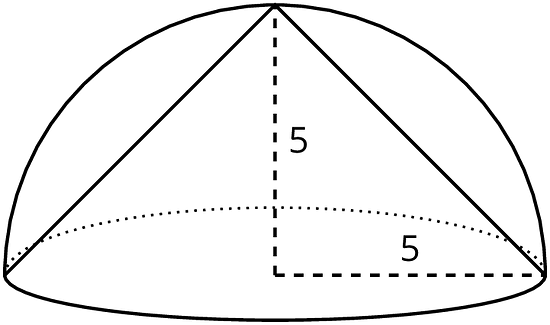
- What is the volume of the cone?
- Estimate the volume of the hemisphere. Explain your reasoning.
- Compare your estimate for the hemisphere with the cone inside to your estimate of the hemisphere inside the cylinder. How do they compare to the volumes of the cylinder and the cone?
Are you ready for more?
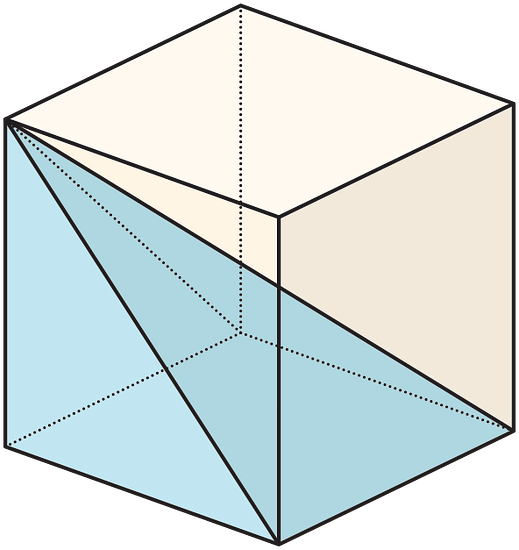
Estimate what fraction of the volume of the cube is occupied by the pyramid that shares the base and a top vertex with the cube, as in the figure.
Lesson 19 Summary
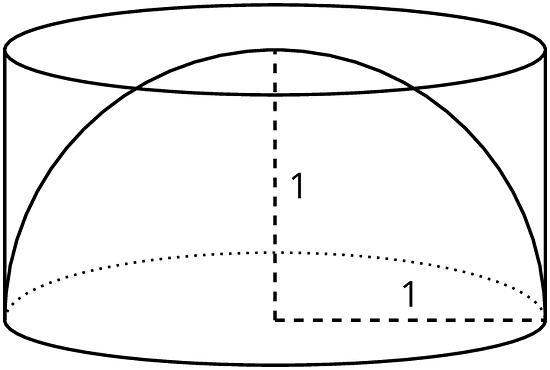
We can estimate the volume of a hemisphere by comparing it to other shapes for which we know the volume. For example, a hemisphere of radius 1 unit fits inside a cylinder with a radius of 1 unit and height of 1 unit.
Since the hemisphere is inside the cylinder, it must have a smaller volume than the cylinder making the cylinder's volume a reasonable over-estimate for the volume of the hemisphere.
The volume of this particular cylinder is about 3.14 units3 since , so we know the volume of the hemisphere is less than 3.14 cubic units.
Using similar logic, a cone of radius 1 unit and height 1 unit fits inside of the hemisphere of radius 1 unit.
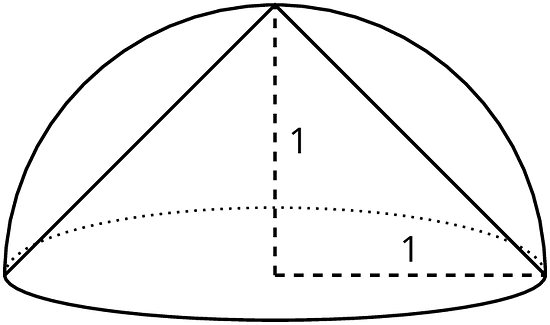
Since the cone is inside the hemisphere, the cone must have a smaller volume than the hemisphere making the cone's volume a reasonable under-estimate for the volume of the hemisphere.
The volume of this particular cone is about 1.05 units3 since , so we know the volume of the hemisphere is more than 1.05 cubic units.
Averaging the volumes of the cylinder and the cone, we can estimate the volume of the hemisphere to be about 2.10 units3 since . And, since a hemisphere is half of a sphere, we can also estimate that a sphere with radius of 1 would be double this volume, or about 4.20 units3.
Lesson 19 Practice Problems
A baseball fits snugly inside a transparent display cube. The length of an edge of the cube is 2.9 inches.
Is the baseball’s volume greater than, less than, or equal to cubic inches? Explain how you know.
There are many possible cones with a height of 18 meters. Let represent the radius in meters and represent the volume in cubic meters.
-
Write an equation that represents the volume as a function of the radius .
-
Complete this table for the function, giving three possible examples.
2 -
If you double the radius of a cone, does the volume double? Explain how you know.
-
Is the graph of this function a line? Explain how you know.
-
A hemisphere fits snugly inside a cylinder with a radius of 6 cm. A cone fits snugly inside the same hemisphere.
- What is the volume of the cylinder?
- What is the volume of the cone?
- Estimate the volume of the hemisphere by calculating the average of the volumes of the cylinder and cone.
-
Find the hemisphere’s diameter if its radius is 6 cm.
-
Find the hemisphere’s diameter if its radius is m.
-
Find the hemisphere’s diameter if its radius is 9.008 ft.
-
Find the hemisphere’s radius if its diameter is 6 cm.
-
Find the hemisphere’s radius if its diameter is m.
-
Find the hemisphere’s radius if its diameter is 9.008 ft.
-
After almost running out of space on her phone, Elena checks with a couple of friends who have the same phone to see how many pictures they have on their phones and how much memory they take up. The results are shown in the table.
number of photos 2,523 3,148 1,875 memory used in MB 8,072 10,106 6,037 - Could this information be reasonably modeled with a linear function? Explain your reasoning.
- Elena needs to delete photos to create 1,200 MB of space. Estimate the number of photos should she delete.