Lesson 11Finding Distances in the Coordinate Plane
Let’s find distances in the coordinate plane.
Learning Targets:
- I can find the distance between two points in the coordinate plane.
- I can find the length of a diagonal line segment in the coordinate plane.
11.1 Closest Distance
- Order the following pairs of coordinates from closest to farthest apart. Be prepared to explain your reasoning.
-
and
-
and
-
and
-
and
-
and
-
-
Name another pair of coordinates that would be closer together than the first pair on your list.
-
Name another pair of coordinates that would be farther apart than the last pair on your list.
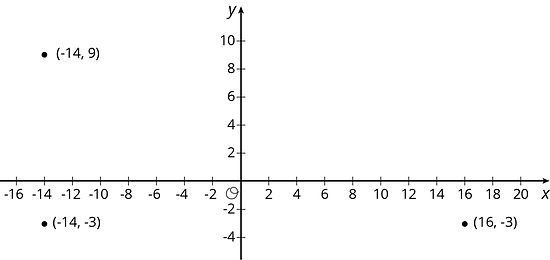
11.2 How Far Apart?
Find the distances between the three points shown.
11.3 Perimeters with Pythagoras
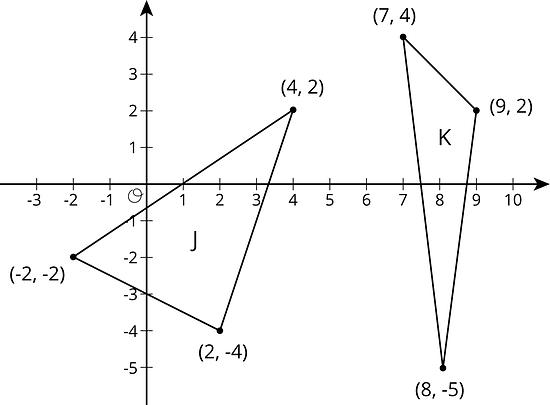
-
Which figure do you think has the longer perimeter?
- Select one figure and calculate its perimeter. Your partner will calculate the perimeter of the other. Were you correct about which figure had the longer perimeter?
Are you ready for more?
Quadrilateral has vertices at , , , and .
- Use the Pythagorean Theorem to find the lengths of sides , , , and .
- Use the Pythagorean Theorem to find the lengths of the two diagonals, and .
-
Explain why quadrilateral is a rectangle.
11.4 Finding the Right Distance
Have each person in your group select one of the sets of coordinate pairs shown here. Then calculate the length of the line segment between those two coordinates. Once the values are calculated, have each person in the group briefly share how they did their calculations.
-
and
-
and
-
and
-
and
- How does the value you found compare to the rest of your group?
-
In your own words, write an explanation to another student for how to find the distance between any two coordinate pairs.
Lesson 11 Summary
We can use the Pythagorean Theorem to find the distance between any two points on the coordinate plane. For example, if the coordinates of point are , and the coordinates of point are , let’s find the distance between them. This distance is also the length of line segment . It is a good idea to plot the points first.
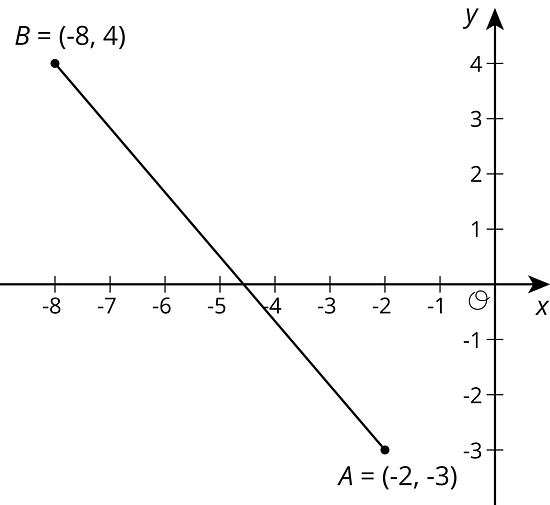
Think of the distance between and , or the length of segment , as the hypotenuse of a right triangle. The lengths of the legs can be deduced from the coordinates of the points.

Once the lengths of the legs are known, we use the Pythagorean Theorem to find the length of the hypotenuse, , which we can represent with . Since is a positive number, there is only one value it can take:
This length is a little longer than 9, since 85 is a little longer than 81. Using a calculator gives a more precise answer, .
Lesson 11 Practice Problems
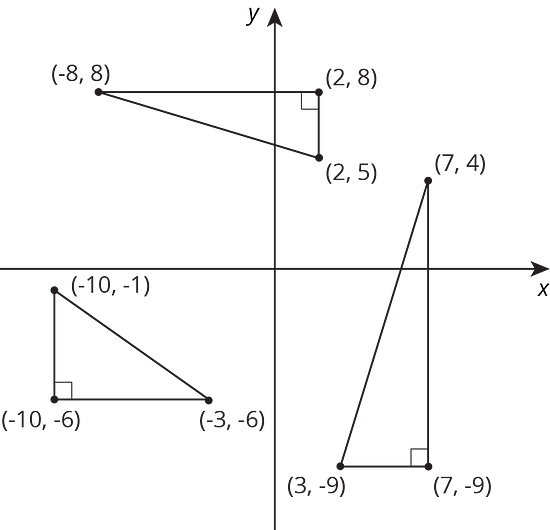
The right triangles are drawn in the coordinate plane, and the coordinates of their vertices are labeled. For each right triangle, label each leg with its length.
Find the distance between each pair of points. If you get stuck, try plotting the points on graph paper.
- and
- and
-
and
Which line has a slope of 0.625, and which line has a slope of 1.6? Explain why the slopes of these lines are 0.625 and 1.6.

Write an equation for the graph.
