Lesson 10Applications of the Pythagorean Theorem
Let’s explore some applications of the Pythagorean Theorem.
Learning Targets:
- I can use the Pythagorean Theorem to solve problems.
10.1 Closest Estimate: Square Roots
Which estimate is closest to the actual value of the expression? Explain your reasoning.
-
-
4
-
4.5
-
5
-
-
-
2
-
2.5
-
3
-
-
-
6
-
6.5
-
7
-
-
+
-
13
-
13.25
-
13.5
-
10.2 Cutting Corners
Mai and Tyler were standing at one corner of a large rectangular field and decided to race to the opposite corner. Since Mai had a bike and Tyler did not, they thought it would be a fairer race if Mai rode along the sidewalk that surrounds the field while Tyler ran the shorter distance directly across the field. The field is 100 meters long and 80 meters wide. Tyler can run at around 5 meters per second, and Mai can ride her bike at around 7.5 meters per second.
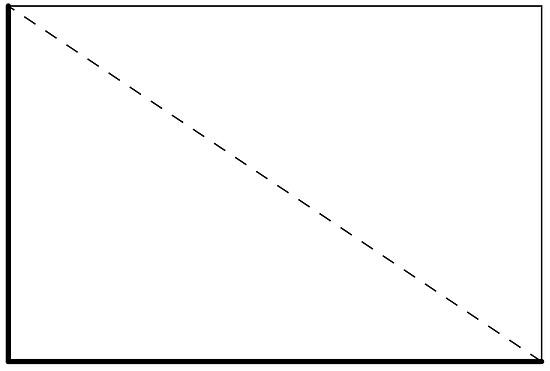
-
Before making any calculations, who do you think will win? By how much? Explain your thinking.
- Who wins? Show your reasoning.
Are you ready for more?
A calculator may be necessary to answer the following questions. Round answers to the nearest hundredth.
-
If you could give the loser of the race a head start, how much time would they need in order for both people to arrive at the same time?
-
If you could make the winner go slower, how slow would they need to go in order for both people to arrive at the same time?
10.3 Internal Dimensions
Here are two rectangular prisms:

- Which figure do you think has the longer diagonal? Note that the figures are not drawn to scale.
- Calculate the lengths of both diagonals. Which one is actually longer?
Lesson 10 Summary
The Pythagorean Theorem can be used to solve any problem that can be modeled with a right triangle where the lengths of two sides are known and the length of the other side needs to be found. For example, let’s say a cable is being placed on level ground to support a tower. It’s a 17-foot cable, and the cable should be connected 15 feet up the tower. How far away from the bottom of the tower should the other end of the cable connect to the ground?
It is often very helpful to draw a diagram of a situation, such as the one shown here:
It’s assumed that the tower makes a right angle with the ground. Since this is a right triangle, the relationship between its sides is , where represents the length of the hypotenuse and and represent the lengths of the other two sides. The hypotenuse is the side opposite the right angle. Making substitutions gives . Solving this for gives . So, the other end of the cable should connect to the ground 8 feet away from the bottom of the tower.
Lesson 10 Practice Problems
A man is trying to zombie-proof his house. He wants to cut a length of wood that will brace a door against a wall. The wall is 4 feet away from the door, and he wants the brace to rest 2 feet up the door. About how long should he cut the brace?
- At a restaurant, a trash can’s opening is rectangular and measures 7 inches by 9 inches. The restaurant serves food on trays that measure 12 inches by 16 inches. Jada says it is impossible for the tray to accidentally fall through the trash can opening because the shortest side of the tray is longer than either edge of the opening. Do you agree or disagree with Jada’s explanation? Explain your reasoning.
Select all the sets that are the three side lengths of right triangles.
-
8, 7, 15
-
4, 10,
-
, 11,
-
, 2,
-
For each pair of numbers, which of the two numbers is larger? How many times larger?
- and
- and
- and
A line contains the point . If the line has negative slope, which of these points could also be on the line?
Noah and Han are preparing for a jump rope contest. Noah can jump 40 times in 0.5 minutes. Han can jump times in minutes, where . If they both jump for 2 minutes, who jumps more times? How many more?