Lesson 9The Converse
Let’s figure out if a triangle is a right triangle.
Learning Targets:
- I can explain why it is true that if the side lengths of a triangle satisfy the equation then it must be a right triangle.
- If I know the side lengths of a triangle, I can determine if it is a right triangle or not.
9.1 The Hands of a Clock
Consider the tips of the hands of an analog clock that has an hour hand that is 3 centimeters long and a minute hand that is 4 centimeters long.

Over the course of a day:
-
What is the farthest apart the two tips get?
-
What is the closest the two tips get?
-
Are the two tips ever exactly five centimeters apart?
9.2 Proving the Converse
Here are three triangles with two side lengths measuring 3 and 4 units, and the third side of unknown length.

Sort the following six numbers from smallest to largest. Put an equal sign between any you know to be equal. Be ready to explain your reasoning.
Are you ready for more?
A similar argument also lets us distinguish acute from obtuse triangles using only their side lengths.
Decide if triangles with the following side lengths are acute, right, or obtuse. In right or obtuse triangles, identify which side length is opposite the right or obtuse angle.
- , ,
- , ,
-
, ,
9.3 Calculating Legs of Right Triangles
- Given the information provided for the right triangles shown here, find the unknown leg lengths to the nearest tenth.
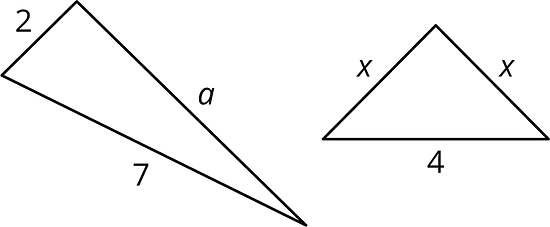
- The triangle shown here is not a right triangle. What are two different ways you change one of the values so it would be a right triangle? Sketch these new right triangles, and clearly label the right angle.
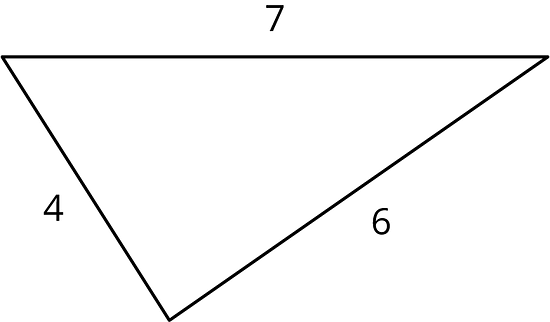
Lesson 9 Summary
What if it isn’t clear whether a triangle is a right triangle or not? Here is a triangle:

Is it a right triangle? It’s hard to tell just by looking, and it may be that the sides aren’t drawn to scale.
If we have a triangle with side lengths , , and , with being the longest of the three, then the converse of the Pythagorean Theorem tells us that any time we have , we must have a right triangle. Since , any triangle with side lengths 8, 15, and 17 must be a right triangle.
Together, the Pythagorean Theorem and its converse provide a one-step test for checking to see if a triangle is a right triangle just using its side lengths. If , it is a right triangle. If , it is not a right triangle.
Lesson 9 Practice Problems
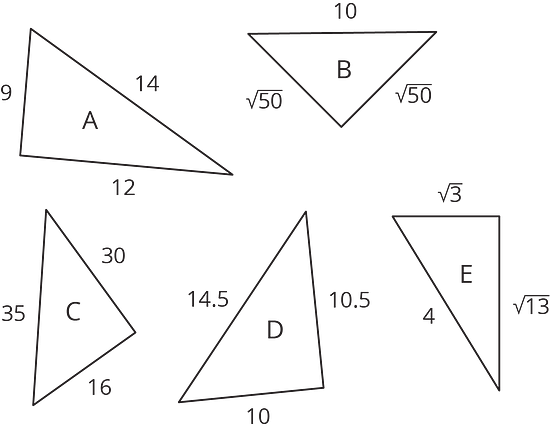
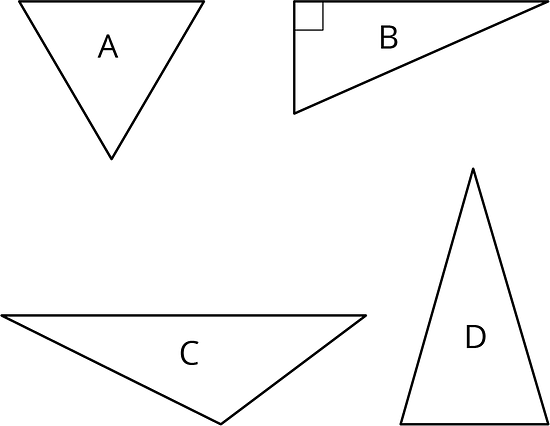
Which of these triangles are definitely right triangles? Explain how you know. (Note that not all triangles are drawn to scale.)
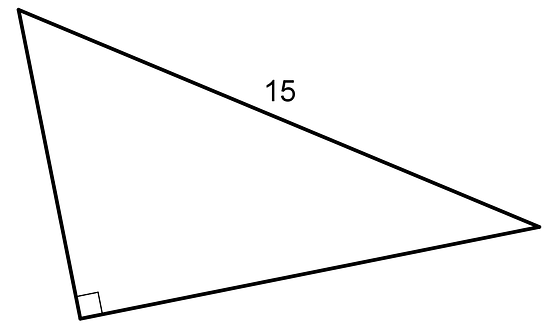
A right triangle has a hypotenuse of 15 cm. What are possible lengths for the two legs of the triangle? Explain your reasoning.
In each part, and represent the length of a leg of a right triangle, and represents the length of its hypotenuse. Find the missing length, given the other two lengths.
For which triangle does the Pythagorean Theorem express the relationship between the lengths of its three sides?
Andre makes a trip to Mexico. He exchanges some dollars for pesos at a rate of 20 pesos per dollar. While in Mexico, he spends 9000 pesos. When he returns, he exchanges his pesos for dollars (still at 20 pesos per dollar). He gets back the amount he started with. Find how many dollars Andre exchanged for pesos and explain your reasoning. If you get stuck, try writing an equation representing Andre’s trip using a variable for the number of dollars he exchanged.