Lesson 13Cube Roots
Let’s compare cube roots.
Learning Targets:
- When I have a cube root, I can reason about which two whole numbers it is between.
13.1 True or False: Cubed
Decide if each statement is true or false.
13.2 Cube Root Values
What two whole numbers does each cube root lie between? Be prepared to explain your reasoning.
13.3 Solutions on a Number Line
The numbers , , and are positive, and:

- Plot , , and on the number line. Be prepared to share your reasoning with the class.
- Plot on the number line.
Are you ready for more?
Diego knows that and that . He says that this means the following are all true:
Lesson 13 Summary
Remember that square roots of whole numbers are defined as side lengths of squares. For example, is the side length of a square whose area is 17. We define cube roots similarly, but using cubes instead of squares. The number , pronounced “the cube root of 17,” is the edge length of a cube which has a volume of 17.
We can approximate the values of cube roots by observing the whole numbers around it and remembering the relationship between cube roots and cubes. For example, is between 2 and 3 since and , and 20 is between 8 and 27. Similarly, since 100 is between and , we know is between 4 and 5. Many calculators have a cube root function which can be used to approximate the value of a cube root more precisely. Using our numbers from before, a calculator will show that and that .
Also like square roots, most cube roots of whole numbers are irrational. The only time the cube root of a number is a whole number is when the original number is a perfect cube.
Lesson 13 Practice Problems
Find the positive solution to each equation. If the solution is irrational, write the solution using square root or cube root notation.
-
For each cube root, find the two whole numbers that it lies between.
- Order the following values from least to greatest:
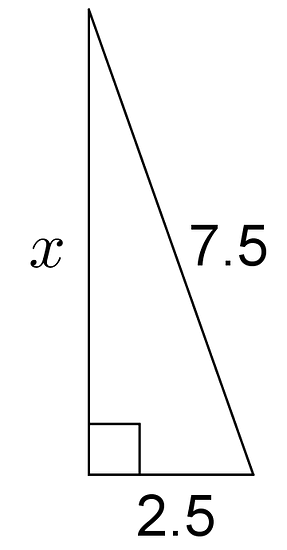
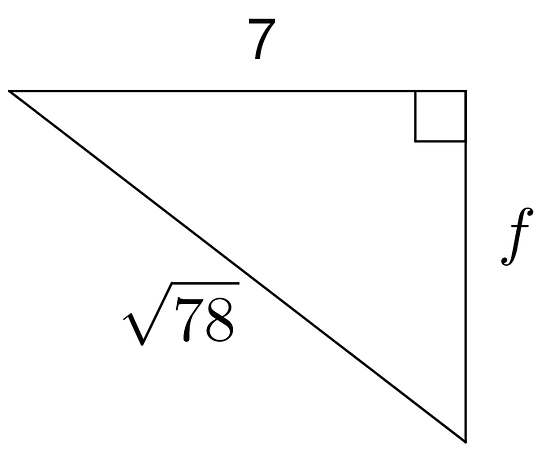
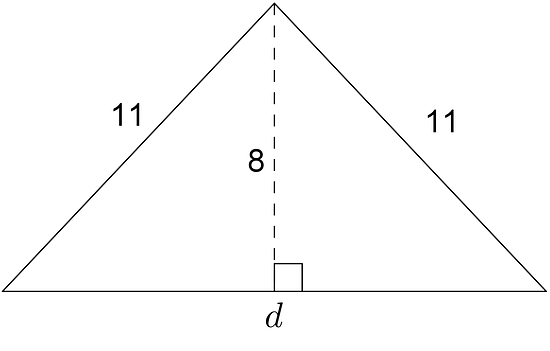
Find the value of each variable, to the nearest tenth.
-
A standard city block in Manhattan is a rectangle measuring 80 m by 270 m. A resident wants to get from one corner of a block to the opposite corner of a block that contains a park. She wonders about the difference between cutting across the diagonal through the park compared to going around the park, along the streets. How much shorter would her walk be going through the park? Round your answer to the nearest meter.