Lesson 14Decimal Representations of Rational Numbers
Let’s learn more about how rational numbers can be represented.
Learning Targets:
- I can write a fraction as a repeating decimal.
- I understand that every number has a decimal expansion.
14.1 Notice and Wonder: Shaded Bars
What do you notice? What do you wonder?

14.2 Halving the Length
Here is a number line from 0 to 1.

- Mark the midpoint between 0 and 1. What is the decimal representation of that number?
- Mark the midpoint between 0 and the newest point. What is the decimal representation of that number?
- Repeat step two. How did you find the value of this number?
- Describe how the value of the midpoints you have added to the number line keep changing as you find more. How do the decimal representations change?
14.3 Recalculating Rational Numbers
-
Rational numbers are fractions and their opposites. All of these numbers are rational numbers. Show that they are rational by writing them in the form or .
- 0.2
- 0.333
- -1.000001
-
-
All rational numbers have decimal representations, too. Find the decimal representation of each of these rational numbers.
14.4 Zooming In On
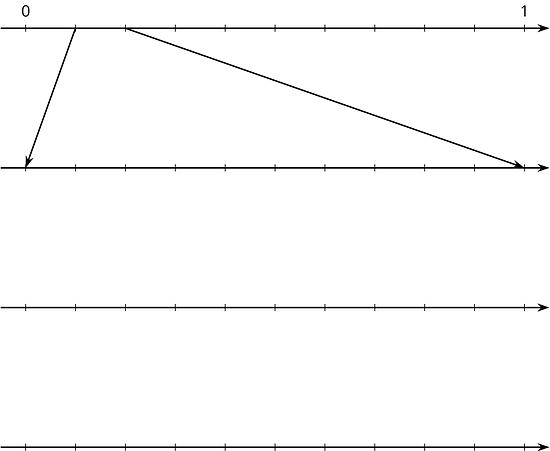
-
On the topmost number line, label the tick marks. Next, find the first decimal place of using long division and estimate where should be placed on the top number line.
-
Label the tick marks of the second number line. Find the next decimal place of by continuing the long division and estimate where should be placed on the second number line. Add arrows from the second to the third number line to zoom in on the location of .
-
Repeat the earlier step for the remaining number lines.
- What do you think the decimal expansion of is?
Are you ready for more?
Let and
For each of the following questions, first decide whether the fraction or decimal representations of the numbers are more helpful to answer the question, and then find the answer.
- Which of or is closer to 2?
-
Find .
Lesson 14 Summary
We learned earlier that rational numbers are a fraction or the opposite of a fraction. For example, and are both rational numbers. A complicated-looking numerical expression can also be a rational number as long as the value of the expression is a positive or negative fraction. For example, and are rational numbers because and .
Rational numbers can also be written using decimal notation. Some have finite decimal expansions, like 0.75, -2.5, or -0.5. Other rational numbers have infinite decimal expansions, like 0.7434343 . . . where the 43s repeat forever. To avoid writing the repeating part over and over, we use the notation for this number. The bar over part of the expansion tells us the part which is to repeat forever.
A decimal expansion of a number helps us plot it accurately on a number line divided into tenths. For example, should be between 0.7 and 0.8. Each further decimal digit increases the accuracy of our plotting. For example, the number is between 0.743 and 0.744.
Lesson 14 Practice Problems
Andre and Jada are discussing how to write as a decimal.
Andre says he can use long division to divide by to get the decimal.
Jada says she can write an equivalent fraction with a denominator of by multiplying by , then writing the number of hundredths as a decimal.
-
Do both of these strategies work?
-
Which strategy do you prefer? Explain your reasoning.
-
Write as a decimal. Explain or show your reasoning.
-
Write each fraction as a decimal.
-
Write each decimal as a fraction.
-
-
0.0276
-
-
10.01
-
Find the positive solution to each equation. If the solution is irrational, write the solution using square root or cube root notation.
-
Here is a right square pyramid.

-
What is the measurement of the slant height of the triangular face of the pyramid? If you get stuck, use a cross section of the pyramid.
-
What is the surface area of the pyramid?
-