Lesson 15Infinite Decimal Expansions
Let’s think about infinite decimals.
Learning Targets:
- I can write a repeating decimal as a fraction.
- I understand that every number has a decimal expansion.
15.1 Searching for Digits
The first 3 digits after the decimal for the decimal expansion of have been calculated. Find the next 4 digits.
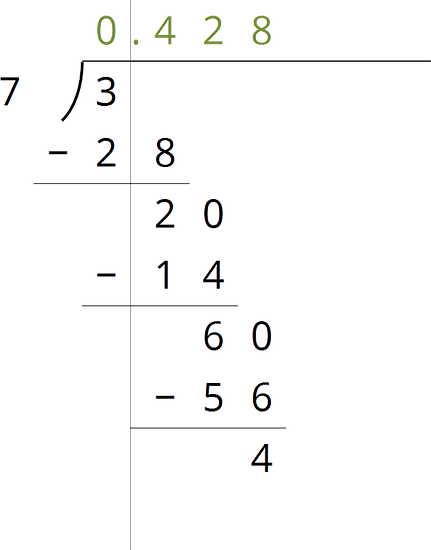
15.2 Some Numbers Are Rational
Your teacher will give your group a set of cards. Each card will have a calculations side and an explanation side.
-
The cards show Noah’s work calculating the fraction representation of . Arrange these in order to see how he figured out that without needing a calculator.
-
Use Noah’s method to calculate the fraction representation of:
Are you ready for more?
Use this technique to find fractional representations for and .
15.3 Some Numbers Are Not Rational
-
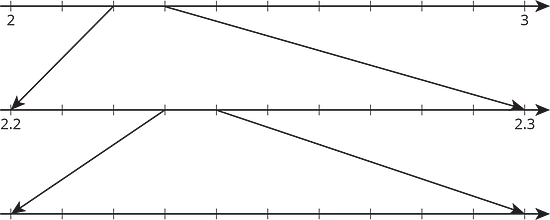
- Why is between 1 and 2 on the number line?
- Why is between 1.4 and 1.5 on the number line?
- How can you figure out an approximation for accurate to 3 decimal places?
-
Label all of the tick marks. Plot on all three number lines. Make sure to add arrows from the second to the third number lines.
-
- Elena notices a beaker in science class says it has a diameter of 9 cm and measures its circumference to be 28.3 cm. What value do you get for using these values and the equation for circumference, ?
- Diego learned that one of the space shuttle fuel tanks had a diameter of 840 cm and a circumference of 2,639 cm. What value do you get for using these values and the equation for circumference, ?
-
Label all of the tick marks on the number lines. Use a calculator to get a very accurate approximation of and plot that number on all three number lines.
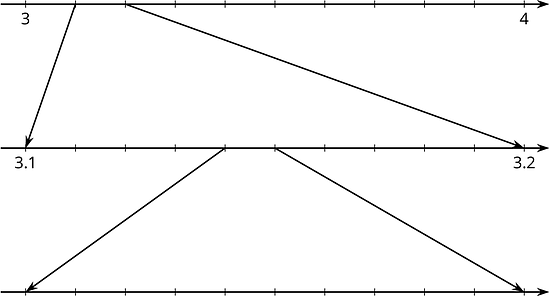
- How can you explain the differences between these calculations of ?
Lesson 15 Summary
Not every number is rational. Earlier we tried to find a fraction whose square is equal to 2. That turns out to be impossible, although we can get pretty close (try squaring ). Since there is no fraction equal to it is not a rational number, which is why we call it an irrational number. Another well-known irrational number is .
Any number, rational or irrational, has a decimal expansion. Sometimes it goes on forever. For example, the rational number has the decimal expansion with the 18s repeating forever. Every rational number has a decimal expansion that either stops at some point or ends up in a repeating pattern like . Irrational numbers also have infinite decimal expansions, but they don't end up in a repeating pattern. From the decimal point of view we can see that rational numbers are pretty special. Most numbers are irrational, even though the numbers we use on a daily basis are more frequently rational.
Lesson 15 Practice Problems
Elena and Han are discussing how to write the repeating decimal as a fraction. Han says that equals . “I calculated because the decimal begins repeating after 3 digits. Then I subtracted to get . Then I multiplied by to get rid of the decimal: . And finally I divided to get .” Elena says that equals . “I calculated because one digit repeats. Then I subtracted to get . Then I did what Han did to get and .”
Do you agree with either of them? Explain your reasoning.
How are the numbers and the same? How are they different?
- Write each fraction as a decimal.
-
-
Write each decimal as a fraction.
-
- Write each fraction as a decimal.
Write each fraction as a decimal.
-
Write each decimal as a fraction.
-
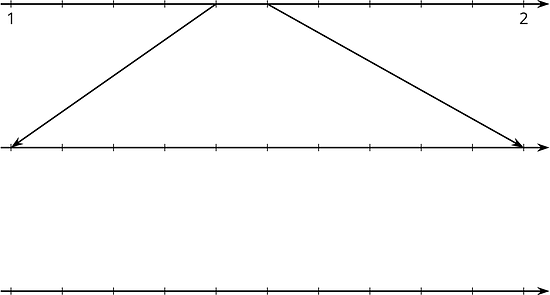
and . This gives some information about .
Without directly calculating the square root, plot on all three number lines using successive approximation.