Open Up Resources Logo

Lesson 4Square Roots on the Number Line

Let’s explore square roots. 

Learning Targets:

  • I can find a decimal approximation for square roots.
  • I can plot square roots on the number line.

4.1 Diagonals

A circle is graphed with center point at (0,0) and radius point at (1,1).
 
  1. What is the exact length of the line segment?
  2. Find a decimal approximation of the length.

4.2 Squaring Lines

  1. Estimate the length of the line segment to the nearest tenth of a unit (each grid square is 1 square unit).
    A line segement is graphed with is 3 units tall and 1 unit wide.
  2. Find the exact length of the segment.

4.3 Square Root of 3

Diego said that he thinks that \sqrt{3}\approx 2.5 .

A square is graphed with a point at (0,0) and (2.5,0).
  1. Use the square to explain why 2.5 is not a very good approximation for  \sqrt{3} . Find a point on the number line that is closer to  \sqrt{3} . Draw a new square on the axes and use it to explain how you know the point you plotted is a good approximation for \sqrt{3} .
  2. Use the fact that \sqrt{3} is a solution to the equation x^2 = 3 to find a decimal approximation of \sqrt{3} whose square is between 2.9 and 3.1.

Are you ready for more?

A farmer has a grassy patch of land enclosed by a fence in the shape of a square with a side length of 4 meters. To make it a suitable home for some animals, the farmer would like to carve out a smaller square to be filled with water, as in the figure.

What should the side length of the smaller square be so that half of the area is grass and half is water?

A square with the side length of 4 is shown with a smaller square inside of it.

Lesson 4 Summary

Here is a line segment on a grid. What is the length of this line segment?

A line segment slanted down from left to right. The right endpoint is 1 unit down and 2 units right from the left endpoint.

By drawing some circles, we can tell that it’s longer than 2 units, but shorter than 3 units.

Two circles that have the same center are drawn on a square grid with radii 2 and 3. A line segment slanted upward and to the left is drawn such that the bottom endpoint is the center of the two circles and is 1 unit down and 2 units right of the top endpoint of the line segment.

To find an exact value for the length of the segment, we can build a square on it, using the segment as one of the sides of the square.

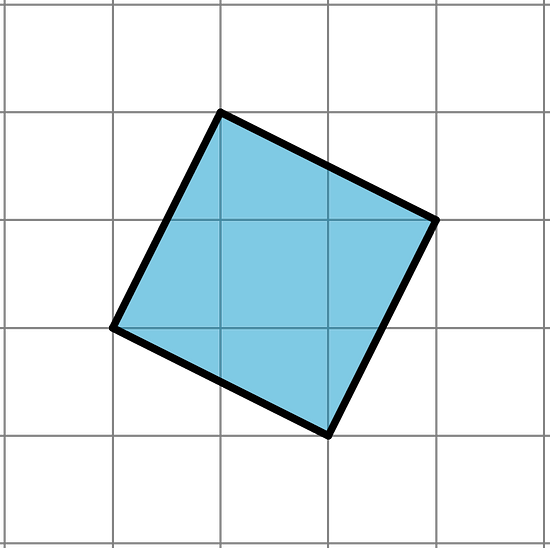
A square on a grid with side lengths equal to the hypotenuse of triangle with side lengths of 1 and 2 units. The square has an area of 5 square units.

The area of this square is 5 square units. (Can you see why?) That means the exact value of the length of its side is \sqrt5 units.

Notice that 5 is greater than 4, but less than 9. That means that \sqrt5 is greater than 2, but less than 3. This makes sense because we already saw that the length of the segment is in between 2 and 3.

With some arithmetic, we can get an even more precise idea of where \sqrt5 is on the number line. The image with the circles shows that \sqrt5 is closer to 2 than 3, so let’s find the value of 2.12 and 2.22 and see how close they are to 5. It turns out that 2.1^2=4.41 and 2.2^2=4.84 , so we need to try a larger number. If we increase our search by a tenth, we find that 2.3^2=5.29 . This means that \sqrt5 is greater than 2.2, but less than 2.3. If we wanted to keep going, we could try 2.25^2 and eventually narrow the value of \sqrt5 to the hundredths place. Calculators do this same process to many decimal places, giving an approximation like \sqrt5 \approx 2.2360679775 . Even though this is a lot of decimal places, it is still not exact because \sqrt5 is irrational.

Lesson 4 Practice Problems

    1. Find the exact length of each line segment.
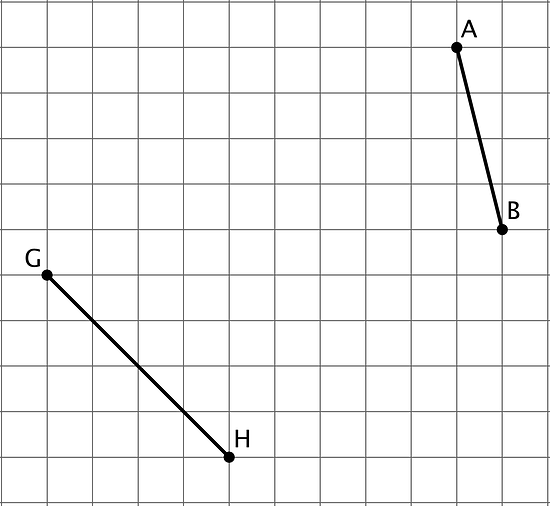
      Line GH is graphed showing a -1 slope. Line AB is graphed with a -0.25 slope.
    2. Estimate the length of each line segment to the nearest tenth of a unit. Explain your reasoning.

  2. Plot each number on the x -axis: \sqrt{16},\text{ } \sqrt{35},\text{ } \sqrt{66} . Consider using the grid to help.

    a bank grid with positive x and y axiis

  3. Use the fact that \sqrt{7} is a solution to the equation x^2 = 7 to find a decimal approximation of \sqrt{7} whose square is between 6.9 and 7.1.

  4. Graphite is made up of layers of graphene. Each layer of graphene is about 200 picometers, or 200 \times 10^{\text-12} meters, thick. How many layers of graphene are there in a 1.6-mm-thick piece of graphite? Express your answer in scientific notation.

  5. Here is a scatter plot that shows the number of assists and points for a group of hockey players. The model, represented by y = 1.5 x + 1.2 , is graphed with the scatter plot. 

    a scatter plot that shows the number of assists and points for a group of hockey players. The model, represented by y=1.5x + 1.2, is graphed with the scatter plot.
    1. What does the slope mean in this situation?
    2. Based on the model, how many points will a player have if he has 30 assists?

  6. The points (12, 23) and (14, 45) lie on a line. What is the slope of the line?