Open Up Resources Logo

Lesson 5Reasoning About Square Roots

Let’s approximate square roots.

Learning Targets:

  • When I have a square root, I can reason about which two whole numbers it is between.

5.1 True or False: Squared

Decide if each statement is true or false.

\left( \sqrt{5} \right)^2=5

\left(\sqrt{9}\right)^2 = 3

7 = \left(\sqrt{7}\right)^2

\left(\sqrt{10}\right)^2 = 100

\left(\sqrt{16}\right)= 2^2

5.2 Square Root Values

What two whole numbers does each square root lie between? Be prepared to explain your reasoning.

  1. \sqrt{7}  
  2. \sqrt{23}  
  3. \sqrt{50}  
  4. \sqrt{98}  

Are you ready for more?

Can we do any better than “between 3 and 4” for  \sqrt{12} ? Explain a way to figure out if the value is closer to 3.1 or closer to 3.9.

5.3 Solutions on a Number Line

The numbers x , y , and z are positive, and x^2 = 3 , y^2 = 16 , and  z^2 = 30 .

A numbre line that shows the integers from negative 3 to 9
  1. Plot x , y , and z on the number line. Be prepared to share your reasoning with the class.
  2. Plot \text- \sqrt{2} on the number line.

Lesson 5 Summary

In general, we can approximate the values of square roots by observing the whole numbers around it, and remembering the relationship between square roots and squares. Here are some examples:

  • \sqrt{65} is a little more than 8, because \sqrt{65} is a little more than \sqrt{64} and \sqrt{64}=8 .
  • \sqrt{80} is a little less than 9, because \sqrt{80} is a little less than \sqrt{81} and \sqrt{81}=9 .
  • \sqrt{75} is between 8 and 9 (it’s 8 point something), because 75 is between 64 and 81.
  • \sqrt{75} is approximately 8.67, because 8.67^2=75.1689 .
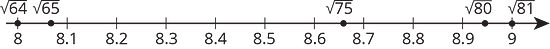
A number line with the numbers 8 through 9, in increments of zero point 1, are indicated. The square root of 64 is indicated at 8. The square root of 65 is indicated between 8 and 8 point 1, where the square root of 65 is closer to 8 point 1. The square root of 75 is indicated between 8 point 6 and 8 point 7, the square root of 75 is closer to 8 point 7. The square root of 80 is indicated between 8 point 9 and 9, where the square root of 80 is closer to 8 point 9. The square root of 81 is indicated at 9.

If we want to find a square root between two whole numbers, we can work in the other direction. For example, since 22^2 = 484 and 23^2 = 529 , then we know that \sqrt{500} (to pick one possibility) is between 22 and 23.

Many calculators have a square root command, which makes it simple to find an approximate value of a square root.

Lesson 5 Practice Problems

    1. Explain how you know that \sqrt{37} is a little more than 6.

    2. Explain how you know that \sqrt{95} is a little less than 10.

    3. Explain how you know that \sqrt{30} is between 5 and 6.

  2. Plot each number on the number line: 6, \sqrt{83}, \sqrt{40}, \sqrt{64}, 7.5

    A number line with 6 evenly spaced tick marks and the integers 5 through 10 are indicated.

  3. Mark and label the positions of two square root values between 7 and 8 on the number line.

    A number line with two tick marks indicated at each end. The number 7 is labeled on the tick mark on the far left and the number 8 is labeled on the tick mark on the far right.

  4. Select all the irrational numbers in the list. \frac23, \frac {\text{-}123}{45}, \sqrt{14}, \sqrt{64}, \sqrt\frac91, \text-\sqrt{99}, \text-\sqrt{100}

  5. Each grid square represents 1 square unit. What is the exact side length of the shaded square?

    A square, not aligned to the horizontal or vertical gridlines, is on a square grid. The square is drawn such that the first vertex of the square is on the left side. The second vertex is 2 grid squares up and 3 grid squares right from the first vertex. The third vertex is 3 grid squares down and 2 grid squares right from the second vertex. The fourth vertex is 2 grid squares down and 3 grid squares left from the third vertex. The first vertex is 3 grid squares up and 2 grid squares left from the fourth vertex.

  6. For each pair of numbers, which of the two numbers is larger? Estimate how many times larger.

    1. 0.37 \boldcdot 10^6 and 700 \boldcdot 10^4
    2. 4.87 \boldcdot 10^4 and 15 \boldcdot 10^5
    3. 500,000 and 2.3 \boldcdot 10^8

  7. The scatter plot shows the heights (in inches) and three-point percentages for different basketball players last season.

    The scatter plot shows the heights (in inches) and three-point percentages for different basketball players last season.
    1. Circle any data points that appear to be outliers.
    2. Compare any outliers to the values predicted by the model.