Open Up Resources Logo

Lección 1Interpretemos números negativos

Repasemos lo que sabemos sobre números con signo.

Metas de aprendizaje:

  • Puedo comparar números racionales.
  • Puedo usar números racionales para describir temperatura y altitud.

1.1 Usemos el termómetro

Este es un termómetro para el clima. Tres de los números se han dejado por fuera.

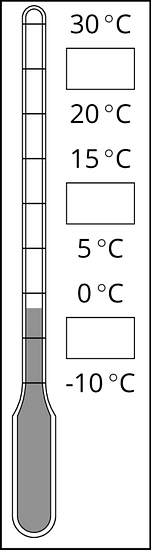
A vertical thermometer measured in degrees Celsius. There are 9 evenly spaced tick marks and starting from the bottom of the thermometer, negative 10 is on the first tick mark, zero on the third, 5 on the fourth, 15 on the sixth, 20 on the seventh, and 30 on the ninth. The second, fifth, and eighth tick marks each are labeled with a box. The thermometer is shaded starting from the bottom of the thermometer to halfway between the second and third tick marks.
  1. ¿Qué números van en las cajas?
  2. ¿Qué temperatura muestra el termómetro?

1.2 Fracciones de un grado

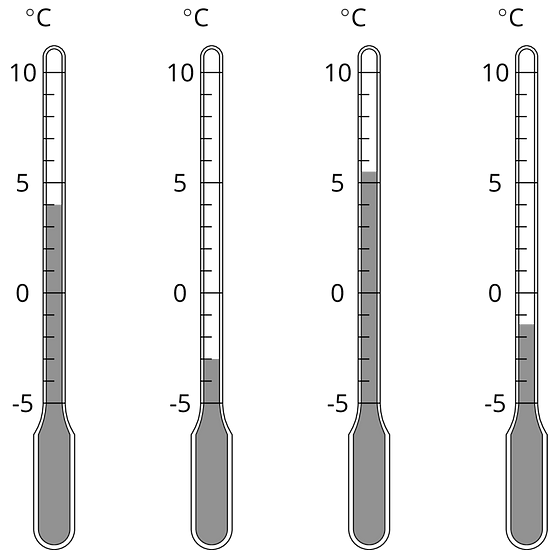
  1. ¿Qué temperatura se muestra en cada termómetro?

  2. ¿Cuál termómetro muestra la mayor temperatura?
  3. ¿Cuál termómetro muestra la menor temperatura?

  4. Supongamos que la temperatura afuera es \text{-}4^\circ \text{C} . ¿Es más fría o más caliente que la temperatura más fría mostrada en la imagen? ¿Cómo lo sabes?

Four vertical thermometers measured in degrees Celsius. There are 16 evenly spaced tick marks and starting from the bottom of the thermometer, negative 5 is on the first tick mark, zero on the sixth, 5 on the eleventh, and 10 on the sixteenth. The first thermometer is shaded starting from the bottom of the thermometer to the tenth tickmark. The second thermometer is shaded starting from the bottom of the thermometer to the third tickmark. The third thermometer is shaded starting from the bottom of the thermometer to between the eleventh and twelfth tickmark. The fourth thermometer is shaded starting from the bottom of the thermometer to between the fourth and fifth tickmark.

1.3 Las gaviotas se elevan, los tiburones nadan

Esta es una imagen de algunos animales marinos. La recta numérica a la izquierda muestra la posición vertical de cada animal por encima o por debajo del nivel del mar, en metros.


 

  1. ¿Cuánto por encima o por debajo del nivel del mar se encuentra cada animal? Mide al nivel de sus ojos.

  2. Una raya mobula esta 3 metros por encima de la superficie del océano. ¿Cómo se compara su distancia hasta la superficie del océano con su distancia vertical hasta los ojos de …

    …el delfín saltarín?

    …la gaviota voladora?

    …el pulpo?

  3. Un albatros está 5 metros por debajo de la superficie del océano. ¿Cómo se compara su distancia hasta la superficie con su distancia vertical hasta los ojos de …

    …el delfín saltarín?

    …la gaviota voladora?

    …el pulpo?

  4. Un pez está 2 metros por debajo de la superficie del océano. ¿Cómo se compara su distancia hasta la superficie con su distancia vertical hasta los ojos de …

    …el delfín saltarín?

    …la gaviota voladora?

    …el pulpo?

  5. La distancia vertical de un nuevo delfín hasta el delfín de la imagen es 3 metros. ¿Cuál es su distancia hasta la superficie del océano?

¿Estás listo para más?

El polo norte está en medio del océano. Una persona al nivel del mar en el polo norte estaría a 3,949 millas del centro de la tierra. El fondo del mar debajo del polo norte está a una altitud aproximada de -2.7 millas. La altitud del polo sur es alrededor de 1.7 millas. ¿Qué tan lejos está una persona parada en el polo sur de un submarino al nivel del mar por debajo del polo norte?

1.4 Clasificación de tarjetas: números racionales

  1. Su profesor le dará al grupo un juego de tarjetas. Ordenen las tarjetas de menor a mayor.
  2. Hagan una pausa aquí para que su profesor pueda revisar su trabajo. Después, su profesor les dará una segundo juego de tarjetas.
  3. Agreguen el nuevo juego de tarjetas al primer juego, de manera que todas las tarjetas queden ordenadas de menor a mayor.

Resumen de la lección 1

Podemos usar números positivos y negativos para representar la temperatura y la altitud.

Cuando los números representan temperaturas, los números positivos indican temperaturas que son más calientes que cero y los números negativos indican temperaturas que son más frías que cero. Este termómetro muestra una temperatura de -1 grado Celsius, que escribimos \text{-}1^\circ \text{C} .

A thermometer positioned horizontally and with the bottom of the thermometer on the left, is labeled “degrees Celsius.” There are 4 evenly spaced large tick marks. Starting on the left, the large tick marks are labeled negative 5, 0, 5, and 10. Between each large tick mark, there are 4 evenly spaced small tick marks. The thermometer is shaded, starting from the left, up to negative 1.

Cuando los números representan altitudes, los números positivos indican posiciones por encima del nivel del mar y los números negativos indican posiciones por debajo del nivel del mar.

Podemos ver el orden de los números con signo en una recta numérica:

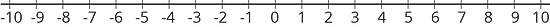
A number line with the numbers negative 10 through 10 indicated.

Un número siempre es menor que los números a su derecha. Así que \text{-}7 < \text{-}3 .

Usamos el valor absoluto para describir qué tan lejos del 0 está un número. Los números 15 y -15 están ambos a 15 unidades del 0, así que |15| = 15 y | \text{-}15| = 15 . Llamamos opuestos a 15 y -15. Están en lados opuestos del 0 en la recta numérica, pero a la misma distancia del 0.

Problemas de práctica de la lección 1

  1. La temperatura era \text- 5 ^\circ \text{C} en Copenhague y  \text- 12 ^\circ \text{C} en Oslo. ¿En qué ciudad estaba haciendo más frío?

    1. Un pez esta 12 metros por debajo de la superficie del océano. ¿Cuál es su altitud?
    2. Un ave marina esta 28 metros por encima de la superficie del océano. ¿Cuál es su altitud?
    3. Si el ave esta directamente por encima del pez, ¿a qué distancia están?

  3. Compara usando >, = o <.

    1. 3 _____ -3
    2. 12 _____ 24
    3. -12 _____ -24
    4. 5 _____ -(-5)
    5. 7.2 _____ 7
    1. -7.2 _____ -7
    2. -1.5 _____ \frac {\text{-}3}{2}
    3. \frac {\text{-}4}{5} _____ \frac {\text{-}5}{4}
    4. \frac {\text{-}3}{5} _____ \frac {\text{-}6}{10}
    5. \frac {\text{-}2}{3} _____ \frac13
  4. Han quiere comprar un boleto de $30 para un partido, pero los boletos de reserva están agotados. Él sabe que habrá más boletos en venta el día del partido, con un aumento de precio del 200%. ¿Cuál es el precio que Han debe esperar pagar por el boleto si lo compra el día del juego?

  5. Un tipo de pintura verde se hace mezclando 2 tazas de amarillo con 3.5 tazas de azul. 

    1. Encuentra una mezcla que haga el mismo tono de verde pero en menor cantidad.

    2. Encuentra una mezcla que haga el mismo tono de verde pero en mayor cantidad. 

    3. Encuentra una mezcla que haga un tono distinto de verde que sea más azul.

    4. Encuentra una mezcla que haga un tono distinto de verde que sea más amarillo.